练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

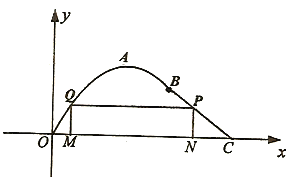
    【题目】（本题16分）某乡镇为了进行美丽乡村建设，规划在长为10千米的河流OC的一侧建一条观光带，观光带的前一部分为曲线段OAB，设曲线段OAB为函数，（单位：千米）的图象，且曲线段的顶点为；观光带的后一部分为线段BC，如图所示.

    （1）求曲线段OABC对应的函数的解析式；

    （2）若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ，绿化带由线段MQ，QP， PN构成，其中点P在线段BC上．当OM长为多少时，绿化带的总长度最长？

    【答案】(1) .

    (2)当OM长为1千米时，绿化带的总长度最长.

    【解析】试题分析：（1）曲线段过点，且最高点为，可列出方程组，求解的值，可得当上函数的解析式，后一部分为线段，，可得上的解析式；（2）求出绿化带的总长度，可得二次函数即可得出结论．

    试题解析：（1）因为曲线段OAB过点O，且最高点为

    ，解得（也可以设成顶点式）

    所以，当时，

    因为后一部分为线段BC，，当时，……6分

    综上，

    （2）设，则

    由， 得，

    所以点

    所以，绿化带的总长度

    ……13分

    当时，

    所以，当OM长为1千米时，绿化带的总长度最长

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当，时，求满足的的值；

    （2）若函数是定义在上的奇函数.

    ①存在，使得不等式有解，求实数的取值范围；

    ②若函数满足，若对任意且，不等式恒成立，求实数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学习小组在暑期社会实践活动中，通过对某商店一种商品销售情况的调查发现：该商品在过去的一个月内（以30天计）的日销售价格（元）与时间（天）的函数关系近似满足（为正常数）.该商品的日销售量（个）与时间（天）部分数据如下表所示：

    （天）

    10

    20

    25

    30

    （个）

    110

    120

    125

    120

    已知第10天该商品的日销售收入为121元.

    （I）求的值;

    （II）给出以下二种函数模型：

    ①，②，

    请你根据上表中的数据，从中选择你认为最合适的一种函数来描述该商品的日销售量与时间的关系，并求出该函数的解析式;

    （III）求该商品的日销售收入（元）的最小值.

    （函数，在区间上单调递减，在区间上单调递增.性质直接应用.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某神奇“黄金数学草”的生长图．第1阶段生长为竖直向上长为1米的枝干，第2阶段在枝头生长出两根新的枝干，新枝干的长度是原来的，且与旧枝成120°，第3阶段又在每个枝头各长出两根新的枝干，新枝干的长度是原来的，且与旧枝成120°，……，依次生长，直到永远．

    （1）求第3阶段“黄金数学草”的高度；

    （2）求第13阶段“黄金数学草”的高度；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（0＜φ＜π）

    （1）当φ时，在给定的坐标系内，用“五点法”做出函数f（x）在一个周期内的图象；

    （2）若函数f（x）为偶函数，求φ的值；

    （3）在（2）的条件下，求函数在[﹣π，π]上的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，对于任意的 ，都有, 当时，，且.

    ( I ) 求的值；

    (II) 当时，求函数的最大值和最小值；

    (III) 设函数，判断函数g(x)最多有几个零点，并求出此时实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)试作出的图象,并根据图象写出的单调区间；

    (2)若函数有两个零点,求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某投资公司计划投资，两种金融产品，根据市场调查与预测，产品的利润与投资金额的函数关系为，产品的利润与投资金额的函数关系为.（注：利润与投资金额单位：万元）

    （1）该公司已有100万元资金，并全部投入，两种产品中，其中万元资金投入产品，试把，两种产品利润总和表示为的函数，并写出定义域；

    （2）试问：怎样分配这100万元资金，才能使公司获得最大利润？其最大利润为多少万元？

    【答案】（1）；（2）20，28.

    【解析】

    （1）设投入产品万元，则投入产品万元，根据题目所给两个产品利润的函数关系式，求得两种产品利润总和的表达式.（2）利用基本不等式求得利润的最大值，并利用基本不等式等号成立的条件求得资金的分配方法.

    （1）其中万元资金投入产品，则剩余的（万元）资金投入产品，

    利润总和为： ，

    （2）因为，

    所以由基本不等式得：,

    当且仅当时，即：时获得最大利润28万.

    此时投入A产品20万元，B产品80万元.

    【点睛】

    本小题主要考查利用函数求解实际应用问题，考查利用基本不等式求最大值，属于中档题.

    【题型】解答题
    【结束】
    20

    【题目】已知曲线.

    （1）求曲线在处的切线方程；

    （2）若曲线在点处的切线与曲线相切，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数满足，且为偶函数，若在内单调递减，则下面结论正确的是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    同步练习册答案