
Ϊ����߲�Ʒ���������ij��ҵ����2013����м����ĸ��������㣬��Ʒ����IJ���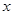 �����Ͷ�뼼���ĸ����
�����Ͷ�뼼���ĸ���� ��Ԫ��
��Ԫ�� ������
������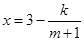 ��
��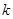 Ϊ��������������㼼���ĸ��ò�Ʒ����IJ���ֻ����1�������֪2013�������ò�Ʒ�Ĺ̶�����Ϊ8��Ԫ��ÿ����1����ò�Ʒ��Ҫ��Ͷ��16��Ԫ�������г�����Ϻã����������IJ�Ʒ�������۳�ȥ�����ҽ�ÿ����Ʒ�����ۼ۸�Ϊÿ����Ʒ�����ɱ���
Ϊ��������������㼼���ĸ��ò�Ʒ����IJ���ֻ����1�������֪2013�������ò�Ʒ�Ĺ̶�����Ϊ8��Ԫ��ÿ����1����ò�Ʒ��Ҫ��Ͷ��16��Ԫ�������г�����Ϻã����������IJ�Ʒ�������۳�ȥ�����ҽ�ÿ����Ʒ�����ۼ۸�Ϊÿ����Ʒ�����ɱ���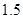 ���������ɱ������̶�Ͷ�����Ͷ���������ʽ𣩣�
���������ɱ������̶�Ͷ�����Ͷ���������ʽ𣩣�
������ȷ����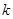 ֵ������2013��ò�Ʒ������
ֵ������2013��ò�Ʒ������ ��Ԫ��ʾΪ�����ĸ����
��Ԫ��ʾΪ�����ĸ���� ��Ԫ�ĺ���������=���۽���D�����ɱ��D�����ĸ���ã���
��Ԫ�ĺ���������=���۽���D�����ɱ��D�����ĸ���ã���
������ҵ2013��ļ����ĸ����Ͷ�������Ԫʱ�����ҵ��������
����y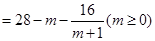 ��
��
������ҵ2013��ļ����ĸ����Ͷ��3��Ԫʱ�����ҵ��������
�����������������������֪����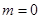 ʱ��
ʱ��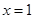 ������
������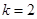 ��
��
����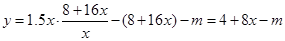 ��
��
Y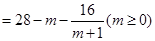 ��
��
����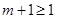 ����
����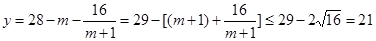 ��
��
���ҽ���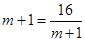 ����
����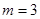 ʱ����ʽȡ�Ⱥţ�
ʱ����ʽȡ�Ⱥţ�
���ԣ�����ҵ2013��ļ����ĸ����Ͷ��3��Ԫʱ�����ҵ��������
���㣺������Ҫ���麯��ģ�ͣ���ֵ������Ӧ�á�
�����������⣬����ʵ��Ӧ�����⣬����������Ļ����ϣ���������ģ�ͣ�Ӧ�õ������ֵ����ȷ����������ֵ�����������Ǹ߿��������ͣ�Ӧ������ע��Ӧ�þ�ֵ������Ҫע�⡰һ��������������ȡ���ȱһ���ɡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
����С������10�֣�ѡ��4-5������ʽѡ��
�� ����
����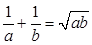 .
.
������ ����Сֵ��
����Сֵ��
�����Ƿ���� ��ʹ��
��ʹ�� ����˵������.
����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�����⽨һ��ƽ��ͼΪ���Σ����Ϊ ������ʽ��ˮ�����أ��ظ�Ϊ1
������ʽ��ˮ�����أ��ظ�Ϊ1 ������ص�����ǽ�ڵĽ���ѵ���Ϊ
������ص�����ǽ�ڵĽ���ѵ���Ϊ Ԫ
Ԫ �����е�ÿ����ǽ��Ȳ��ƣ����ֻ��һ�棬��ǽ�Ľ���ѵ���Ϊ
�����е�ÿ����ǽ��Ȳ��ƣ����ֻ��һ�棬��ǽ�Ľ���ѵ���Ϊ Ԫ
Ԫ ���صĽ���ѵ���Ϊ
���صĽ���ѵ���Ϊ Ԫ
Ԫ ����ˮ�صij������ֱ�Ϊ������ʱ����ˮ�ص������ͣ�������Ϊ����Ԫ��
����ˮ�صij������ֱ�Ϊ������ʱ����ˮ�ص������ͣ�������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ijʳƷ�����ڹ�����ۣ���֪�ó�ÿ����Ҫ���6�֣�ÿ����۵ļ۸�Ϊ3200Ԫ����۵ı��ܵ���������Ϊƽ��ÿ��ÿ��3Ԫ���������ÿ����Ҫ ֧���˷�900Ԫ��
֧���˷�900Ԫ��
������ó�ÿ�������칺��һ����ۣ�����ʹƽ��ÿ��֧�����ܷ��� ���٣����ٷ���Ϊ���٣�
���٣����ٷ���Ϊ���٣�
����ij�ṩ��۵Ĺ�˾�涨����һ�ι�����۲�����120��ʱ���۸������9.5���Żݣ��ʸó��Ƿ������ô��Ż���������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��x��y����Լ������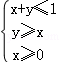 ����z=2x��y�����ֵΪ�� ��.
����z=2x��y�����ֵΪ�� ��.
| A��0 | B��2 | C��3 | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��ʵ��x, ���㲻��ʽ��
���㲻��ʽ��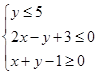 ����z=|x|+2
����z=|x|+2 �����ֵ�ǣ� ��
�����ֵ�ǣ� ��
| A��10 | B��11 | C��13 | D��14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
����ʽ�� ��ʾ��ƽ��������(����)
��ʾ��ƽ��������(����)
| A������ | B�������� | C��ֱ������ | D���������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com