
【题目】某水果经销商为了对一批刚上市水果进行合理定价,将该水果按事先拟定的价格进行试销,得到一组销售数据,如表所示:
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
(1)已知变量![]() 具有线性相关关系,求该水果日销售量
具有线性相关关系,求该水果日销售量![]() (公斤)关于试销单价
(公斤)关于试销单价![]() (元/公斤)的线性回归方程,并据此分析销售单价
(元/公斤)的线性回归方程,并据此分析销售单价![]() 时,日销售量的变化情况;
时,日销售量的变化情况;
(2)若该水果进价为每公斤![]() 元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价
元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价![]()
![]() 应定为多少元?
应定为多少元?
(参考数据及公式:![]() ,
,![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,
,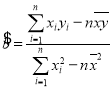 ,
,![]() )
)
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋内有大小完全相同的![]() 个黑球和
个黑球和![]() 个白球,从中不放回地每次任取
个白球,从中不放回地每次任取![]() 个小球,直至取到白球后停止取球,则( )
个小球,直至取到白球后停止取球,则( )
A.抽取![]() 次后停止取球的概率为
次后停止取球的概率为![]()
B.停止取球时,取出的白球个数不少于黑球的概率为![]()
C.取球次数![]() 的期望为
的期望为![]()
D.取球次数![]() 的方差为
的方差为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为![]() ,客场取胜的概率为
,客场取胜的概率为![]() ,且各场比赛结果相互独立,则甲队不超过
,且各场比赛结果相互独立,则甲队不超过![]() 场即获胜的概率是( )
场即获胜的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将n×n的棋盘的部分结点(单位正方形的顶点)染红,使得任意一个由单位正方形构成的k×k![]() 的子棋盘的边界上至少有一个红点.记满足条件的红点数的最小值为
的子棋盘的边界上至少有一个红点.记满足条件的红点数的最小值为![]() . 试求
. 试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的点A(4,t)到其焦点F的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F作直线l,使得抛物线C上恰有三个点到直线1的距离为2,求直线1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每卦有三根线组成(“![]() ”表示一根阳线,“
”表示一根阳线,“![]() ”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.
”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com