【题目】袋内有大小完全相同的
个黑球和
个白球，从中不放回地每次任取
个小球，直至取到白球后停止取球，则（ ）
A.抽取次后停止取球的概率为
B.停止取球时，取出的白球个数不少于黑球的概率为
C.取球次数
的期望为
D.取球次数的方差为
口算题卡加应用题集训系列答案
综合自测系列答案科目：高中数学 来源： 题型：
【题目】“日行一万步，健康你一生”的养生观念已经深入人心，由于研究需要，某学生收集了“微信运动”中100名成员一天的行走步数，对这100个数据按组距为2500进行分组，并统计整理，绘制了如下尚不完整的统计表：
步数分组统计表（设步数为
）
组别 | 步数分组 | 频数 |
|
| 10 |
|
|
|
|
| 20 |
|
| 10 |
|
|
|
已知达到“日行一万步，健康你一生”标准的频率为
.
（1）求
，
的值；
（2）以频率估计概率，从该“微信运动”中任意抽取3名成员，记其中达到“日行一万步，健康你一生”标准的人数为
，求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，过椭圆的焦点且与长轴垂直的弦长为1．
（1）求椭圆C的方程；
（2）设点M为椭圆上第一象限内一动点，A，B分别为椭圆的左顶点和下顶点，直线MB与x轴交于点C，直线MA与y轴交于点D，求证：四边形ABCD的面积为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某水果经销商为了对一批刚上市水果进行合理定价，将该水果按事先拟定的价格进行试销，得到一组销售数据，如表所示：
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
（1）已知变量
具有线性相关关系，求该水果日销售量
（公斤）关于试销单价
（元/公斤）的线性回归方程，并据此分析销售单价
时，日销售量的变化情况；
（2）若该水果进价为每公斤
元，预计在今后的销售中，日销售量和售价仍然服从（1）中的线性相关关系，该水果经销商如果想获得最大的日销售利润，此水果的售价
应定为多少元？
（参考数据及公式：
，
，
，线性回归方程
，
，
）
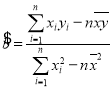查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝ex(ax＋b)－x2－4x，曲线y＝f(x)在点(0，f(0))处的切线方程为y＝4x＋4．
(Ⅰ)求a，b的值；
(Ⅱ)讨论f(x)的单调性．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】请你设计一个包装盒，如图所示，
是边长为
的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得
四个点重合于图中的点
，正好形成一个正四棱柱形状的包装盒，
在
上，是被切去的一个等腰直角三角形斜边的两个端点，设
(
).
（1）某广告商要求包装盒的侧面积
最大，试问
应取何值？
（2）某厂商要求包装盒的容积
最大，试问应取何值？并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
