练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《易经》是中国传统文化中的精髓，下图是易经八卦图（含乾、坤、巽、震、坎、离、艮、兑八卦），每卦有三根线组成（“”表示一根阳线，“”表示一根阴线），从八卦中任取两卦，这两卦的六根线中恰有三根阳线和三根阴线的概率__________．

    【答案】

    【解析】

    由图可得：三根都是阳线的有一卦，三根都是阴线的有一卦，两根阳线一根阴线的有三卦，两根阴线一根阳线的有三卦，利用组合数可得基本事件总数，分类利用计算原理求得符合要求的基本事件个数为10个，问题得解.

    从八卦中任取两卦，共有种取法

    若两卦的六根线中恰有三根阳线和三根阴线，可按取得卦的阳、阴线的根数分类计算；

    当有一卦阳、阴线的根数为3、0时，另一卦阳、阴线的根数为0、3，共有种取法.

    当有一卦阳、阴线的根数为2、1时，另一卦阳、阴线的根数为1、2，共有种取法.

    所以两卦的六根线中恰有三根阳线和三根阴线的取法有种.

    则从八卦中任取两卦，这两卦的六根线中恰有三根阳线和三根阴线的概率为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某水果经销商为了对一批刚上市水果进行合理定价，将该水果按事先拟定的价格进行试销，得到一组销售数据，如表所示：

    试销单价（元/公斤）

    16

    17

    18

    19

    20

    日销售量（公斤）

    168

    146

    120

    90

    56

    （1）已知变量具有线性相关关系，求该水果日销售量（公斤）关于试销单价（元/公斤）的线性回归方程，并据此分析销售单价时，日销售量的变化情况；

    （2）若该水果进价为每公斤元，预计在今后的销售中，日销售量和售价仍然服从（1）中的线性相关关系，该水果经销商如果想获得最大的日销售利润，此水果的售价应定为多少元？

    （参考数据及公式：，，，线性回归方程，，）

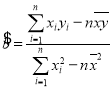    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点P（－1，0），设不垂直于x轴的直线l与抛物线y2＝2x交于不同的两点A、B，若x轴是∠APB的角平分线，则直线l一定过点

    A. （，0） B. （1，0） C. （2，0） D. （-2，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】请你设计一个包装盒，如图所示，是边长为的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得四个点重合于图中的点，正好形成一个正四棱柱形状的包装盒，在上，是被切去的一个等腰直角三角形斜边的两个端点，设().

    （1）某广告商要求包装盒的侧面积最大，试问应取何值？

    （2）某厂商要求包装盒的容积最大，试问应取何值？并求出此时包装盒的高与底面边长的比值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校社团为调查学生课余学习围棋的情况，随机抽取了100名学生进行调查．根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示，将日均学习围棋时间不低于40分钟的学生称为“围棋迷”．

    根据已知条件完成下面的列联表，并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关？

    非围棋迷

    围棋迷

    总计

    男

    女

    10

    55

    总计

    附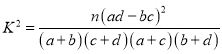：，其中．

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小赵和小王约定在早上至之间到某公交站搭乘公交车去上学，已知在这段时间内，共有班公交车到达该站，到站的时间分别为，，如果他们约定见车就搭乘，则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某汽车公司对最近6个月内的市场占有率进行了统计，结果如表；

    月份代码

    1

    2

    3

    4

    5

    6

    市场占有率

    11

    13

    16

    15

    20

    21

    (1)可用线性回归模型拟合与之间的关系吗?如果能,请求出关于的线性回归方程,如果不能,请说明理由;

    (2)公司决定再采购两款车扩大市场, 两款车各100辆的资料如表：

    车型

    报废年限（年）

    合计

    成本

    1

    2

    3

    4

    10

    30

    40

    20

    100

    1000元/辆

    15

    40

    35

    10

    100

    800元/辆

    平均每辆车每年可为公司带来收入元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年，用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?

    参考数据: ，，，.

    参考公式:相关系数；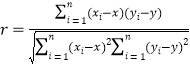

    回归直线方程为,其中，.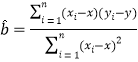

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，平面，，，，点在线段上，且，为线段的中点.

    （1）求证：平面；

    （2）若，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    若是函数的极值点，求实数a的值；

    若对任意的为自然对数的底数，都有成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案