【题目】《算法统宗》是我国古代数学名著．在这部著作中，许多数学问题都是以歌诀形式呈现的，“竹筒容米”就是其中一首：家有八节竹一茎，为因盛米不均平；下头三节三生九，上梢三节贮三升；唯有中间二节竹，要将米数次第盛；若是先生能算法，也教算得到天明！大意是：用一根8节长的竹子盛米，每节竹筒盛米的容积是不均匀的，下端3节可盛米3.9升，上端3节可盛米3升．要按依次盛米容积相差同一数量的方式盛米，中间两节可盛米多少升？由以上条件，计算出这根八节竹筒的容积为（ ）
A. 
升 B. 
升 C. 
升 D. 
升
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号，某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传，要求版心面积为162 
（版心是指图中的长方形阴影部分，
为长度单位分米），上、下两边各空2 ，左、右两边各空1 .
（1）若设版心的高为
，求海报四周空白面积关于
的函数
的解析式；
（2）要使海报四周空白面积最小，版心的高和宽该如何设计？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1是四棱锥的直观图，其正(主)视图和侧(左)视图均为直角三角形，俯视图外框为矩形，相关数据如图2所示.
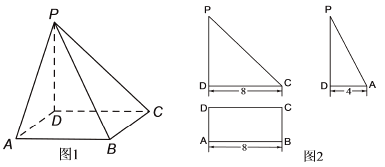
(1)设
中点为
，在直线
上找一点
，使得
平面
，并说明理由；
(2)若二面角
的平面角的余弦值为
，求四棱锥
的外接球的表面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的极坐标方程为
,以极点为原点, 极轴为
轴的正半轴, 建立平面直角坐标系, 直线
的参数方程为
为参数）．
（1）判断直线与曲线的位置关系, 并说明理由；
（2）若直线与曲线相交于
两点, 且
,求直线的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：y2=2px（p＞0）的焦点为F并且经过点A（1，﹣2）．
（1）求抛物线C的方程；
（2）过F作倾斜角为45°的直线l，交抛物线C于M，N两点，O为坐标原点，求△OMN的面积。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了了解某地高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12．
（1）第二小组的频率是多少？样本容量是多少？
（2）若次数在110以上为达标，试估计全体高一学生的达标率为多少？
（3）通过该统计图，可以估计该地学生跳绳次数的众数是______，中位数是_______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某汽车美容公司为吸引顾客，推出优惠活动：对首次消费的顾客，按
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠，标准如下：
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为
元, 根据所给数据, 解答下列问题:
（1）估计该公司一位会员至少消费两次的概率；
（2）某会员仅消费两次, 求这两次消费中, 公司获得的平均利润；
（3）以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为
元, 求
的分布列和数学期望
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
