
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
(2)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 上的零点个数.
上的零点个数.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用题意消元,配方得到二次函数的对称轴,讨论对称轴与所给区间上的关系进行求解;(2)先化简得到一元二次方程,再利用分类讨论思想对判别式进行讨论求解.
试题解析:(1)当![]() 时,
时,
![]() ,对称轴为直线
,对称轴为直线![]() .
.
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() .………………1分
.………………1分
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
且![]() ,所以
,所以![]() .………………2分
.………………2分
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
且![]() ,所以
,所以![]() .………………3分
.………………3分
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() .
.
综上所述,![]() .………………4分
.………………4分
(2)当![]() 时,
时,![]() .
.
令![]() ,即
,即![]() ,
,
解得![]() 或
或![]() .………………5分
.………………5分
当![]() 时,
时,![]() ,即
,即![]() .
.
因为![]() ,
,
所以当![]() 即
即![]() 时,方程
时,方程![]() 有两个实数解.………………6分
有两个实数解.………………6分
当![]() 即
即![]() 时,方程
时,方程![]() 有且只有一个实数解
有且只有一个实数解![]() .………………7分
.………………7分
当![]() 即
即![]() 时,方程
时,方程![]() 没有实数解.………………8分
没有实数解.………………8分
当![]() 时,
时,![]() ,即
,即![]() .
.
因为![]() ,
,
所以当![]() 即
即![]() 时,方程
时,方程![]() 有两个实数解.………………9分
有两个实数解.………………9分
当![]() 即
即![]() 时,方程
时,方程![]() 有且只有一个实数解
有且只有一个实数解![]() .………………10分
.………………10分
当![]() 即
即![]() 时,方程
时,方程![]() 没有实数解.………………11分
没有实数解.………………11分
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 上的零点个数是4;
上的零点个数是4;
当![]() 时,函数
时,函数![]() 在
在![]() 上的零点个数是3;
上的零点个数是3;
当![]() 时,函数
时,函数![]() 在
在![]() 上的零点个数是2;
上的零点个数是2;
当![]() 时,函数
时,函数![]() 在
在![]() 上的零点个数是1;
上的零点个数是1;
当![]() 时,函数
时,函数![]() 在
在![]() 上的零点个数是0.………………12分
上的零点个数是0.………………12分


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】《算法统宗》是我国古代数学名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“竹筒容米”就是其中一首:家有八节竹一茎,为因盛米不均平;下头三节三生九,上梢三节贮三升;唯有中间二节竹,要将米数次第盛;若是先生能算法,也教算得到天明!大意是:用一根8节长的竹子盛米,每节竹筒盛米的容积是不均匀的,下端3节可盛米3.9升,上端3节可盛米3升.要按依次盛米容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出这根八节竹筒的容积为( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式:

查看答案和解析>>
科目:高中数学 来源: 题型:
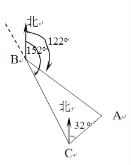
【题目】如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为![]() 的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为
的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为![]() .半小时后,货轮到达C点处,观测到灯塔A的方位角为
.半小时后,货轮到达C点处,观测到灯塔A的方位角为![]() .求此时货轮与灯塔之间的距离.
.求此时货轮与灯塔之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)记![]() ,那么当
,那么当![]() 时,是否存在区间
时,是否存在区间![]() 使得函数在区间
使得函数在区间![]() 上的值域恰好为
上的值域恰好为![]() ?若存在,请求出区间
?若存在,请求出区间![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由
交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=![]() a,
a,
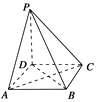
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com