
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
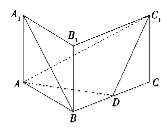
⑴求证:![]() ;
;
⑵求二面角![]() 的余弦值;
的余弦值;
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的![]() ,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
,部分对应值如表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的命题;
的命题;
|
|
|
|
|
|
|
|
|
|
|
|
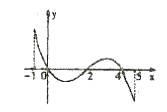
①函数![]() 的值域为
的值域为![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③如果当![]() 时,
时, ![]() 最大值是
最大值是![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;
;
④当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.
其中正确命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
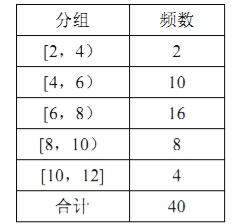
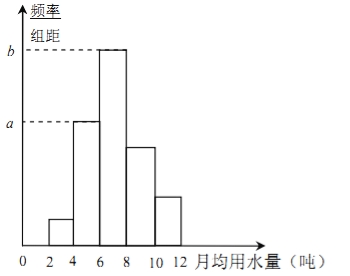
(1)求频率分布直方图中![]() 的值;
的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com