
【题目】2018年10月24日,世界上最长的跨海大桥—港珠澳大桥正式通车。在一般情况下,大桥上的车流速度v(单位:千米/时)是车流密度x(单位:辆/千米)的函数当桥上的车流密度达到220辆/千米,将造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米,车流速度为100千米/时研究表明:当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时)![]() 可以达到最大?并求出最大值.
可以达到最大?并求出最大值.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于15小时,也不超过40小时,设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元,在乙家租一张球台开展活动
元,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元.
元.
(1)写出![]() 与
与![]() 的解析式;
的解析式;
(2)选择哪家比较合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一张长为80cm、宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面正方形边长为x(cm),高为y(cm),体积为V(cm3).求:
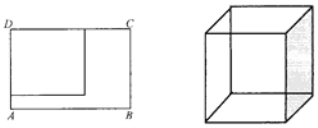
(1)y关于x的表达式;
(2)该铁皮盒体积V的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用一半径为4cm的圆形纸片(圆心为O)制作一个正四棱锥.方法如下:
(1)以O为圆心制作一个小的圆;
(2)在小的圆内制作一内接正方形ABCD;
(3)以正方形ABCD的各边向外作等腰三角形,使等腰三角形的顶点落在大圆上(如图);
(4)将正方形ABCD作为正四棱锥的底,四个等腰三角形作为正四棱锥的侧面折起,使四个等腰三角形的顶点重合,问:要使所制作的正四棱锥体积最大,则小圆的半径为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为![]() ,则它们的大小关系为( )
,则它们的大小关系为( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)设数列![]() 的前
的前![]() 项和为
项和为![]() .已知
.已知![]() ,
, ![]() ,
, ![]() .
.
(1)写出![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;
;
(3)若数列![]() 满足
满足![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车驾驶学校在学员结业前,对学员的驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核。若学员小李独立参加每次考核合格的概率依次组成一个公差为![]() 的等差数列,他参加第一次考核合格的概率不超过
的等差数列,他参加第一次考核合格的概率不超过![]() ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为![]() .
.
(1)求小李第一次参加考核就合格的概率![]() ;
;
(2)求小李参加考核的次数![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com