
【题目】新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车、其他新能源汽车等.它是未来汽车的发展方向.一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线,这条流水线生产的新能源汽车数量![]() (辆)与创造的价值
(辆)与创造的价值![]() (万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
(万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足:
满足:![]() ,
,![]() 的最小值为1,且在
的最小值为1,且在![]() 轴上的截距为4.
轴上的截距为4.
(1)求此二次函数![]() 的解析式;
的解析式;
(2)若存在区间![]() ,使得函数
,使得函数![]() 的定义域和值域都是区间
的定义域和值域都是区间![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的“不变区间”.试求函数
的“不变区间”.试求函数![]() 的不变区间;
的不变区间;
(3)若对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() ,圆
,圆![]() 的方程是
的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上任意一点
上任意一点![]() 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,
的部分图象如图所示,![]()
![]() 分别是图象的最高点与相邻的最低点,且
分别是图象的最高点与相邻的最低点,且![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图象向左平移1个单位后得到函数
的图象向左平移1个单位后得到函数![]() 的图象,求函数
的图象,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的图象的相邻两条对称轴之间的距离为4,且有一个零点为
)的图象的相邻两条对称轴之间的距离为4,且有一个零点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
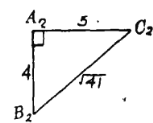
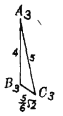
【题目】现有边长分别3,4,5的三角形两个,边长分别4,5,![]() 的三角形四个,边长分别为
的三角形四个,边长分别为![]() ,4,5的三角形六个.用上述三角形为面,可以拼成______个四面体.
,4,5的三角形六个.用上述三角形为面,可以拼成______个四面体.
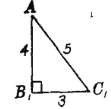
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下关于线性方程组解的个数的命题.
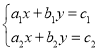 ①,
①,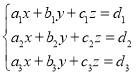 ②,
②,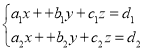 ③,
③, ④,
④,
(1)方程组①可能有无穷多组解;
(2)方程组②可能有且只有两组不同的解;
(3)方程组③可能有且只有唯一一组解;
(4)方程组④可能有且只有唯一一组解.
其中真命题的序号为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足:①对于任意的正整数
同时满足:①对于任意的正整数![]() ,
, ![]() 恒成立;②对于给定的正整数
恒成立;②对于给定的正整数![]() ,
, ![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,则称数列
恒成立,则称数列![]() 是“
是“![]() 数列”.
数列”.
(1)已知![]() 判断数列
判断数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(2)已知数列![]() 是“
是“![]() 数列”,且存在整数
数列”,且存在整数![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,证明:
成等差数列,证明: ![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com