
【题目】已知非空集合M满足M{0,1,2,…,n}(n≥2,n∈N+).若存在非负整数k(k≤n),使得当a∈M时,均有2k﹣a∈M,则称集合M具有性质P.设具有性质P的集合M的个数为f(n).
(1)求f(2)的值;
(2)求f(n)的表达式.
【答案】
(1)解:当n=2时,M={0},{1},{2},{0,2},{0,1,2}具有性质P,
对应的k分别为0,1,2,1,1,故f(2)=5.
(2)解:可知当n=k时,具有性质P的集合M的个数为f(t),
则当n=k+1时,f(t+1)=f(t)+g(t+1),
其中g(t+1)表达t+1∈M也具有性质P的集合M的个数,
下面计算g(t+1)关于t的表达式,
此时应有2k≥t+1,即 ![]() ,故对n=t分奇偶讨论,
,故对n=t分奇偶讨论,
①当t为偶数时,t+1为奇数,故应该有 ![]() ,
,
则对每一个k,t+1和2k﹣t﹣1必然属于集合M,且t和2k﹣t,…,k和k共有t+1﹣k组数,每一组数中的两个数必然同时属于或不属于集合M,
故对每一个k,对应的具有性质P的集合M的个数为 ![]() ,
,
所以 ![]() ,
,
②当t为奇数时,t+1为偶数,故应该有 ![]() ,
,
同理 ![]() ,
,
综上,可得 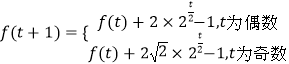 又f(2)=5,
又f(2)=5,
由累加法解得 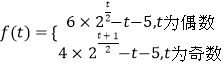
即 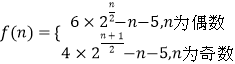
【解析】(1)当n=2时,M={0},{1},{2},{0,2},{0,1,2}具有性质P,求出对应的k,即可得出.(2)可知当n=k时,具有性质P的集合M的个数为f(t),当n=k+1时,f(t+1)=f(t)+g(t+1),其中g(t+1)表达t+1∈M也具有性质P的集合M的个数,
计算g(t+1)关于t的表达式,此时应有2k≥t+1,即 ![]() ,故对n=t分奇偶讨论,利用集合M具有性质P即可得出.
,故对n=t分奇偶讨论,利用集合M具有性质P即可得出.
【考点精析】解答此题的关键在于理解集合的表示方法-特定字母法的相关知识,掌握①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.


科目:高中数学 来源: 题型:
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1m的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形,现计划将矩形ABCD区域设计为可推拉的窗口. 
(1)若窗口ABCD为正方形,且面积大于 ![]() m2(木条宽度忽略不计),求四根木条总长的取值范围;
m2(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为6m,求窗口ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ,现建立以
,现建立以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系.
轴的正半轴为极轴的极坐标系.
(1)写出直线![]() 极坐标方程,曲线
极坐标方程,曲线![]() 的参数方程;
的参数方程;
(2)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏. 
(1)若当∠OBC= ![]() 时,sin∠BCO=
时,sin∠BCO= ![]() ,求此时a的值;
,求此时a的值;
(2)设y=CA2+CB2 , 且CA2+CB2≤232.
(i)试将y表示为a的函数,并求出a的取值范围;
(ii)若同时要求市民在水池边缘任意一点C处观赏喷泉时,观赏角度∠ACB的最大值不小于 ![]() ,试求A,B两处喷泉间距离的最小值.
,试求A,B两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点. 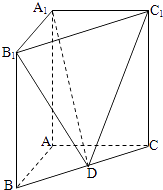
(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间(t),结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间t(分钟/人) | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末已准备好了工具的顾客人数,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com