

(1)求曲线F的方程;
(2)求证:直线l与曲线F只有一个公共点M;
(3)若r=4,点M在第一象限,且![]() ,记直线l与直线CM的夹角为
,记直线l与直线CM的夹角为![]() ,
,
求tan![]() .
.
解:(1)连接MB,由题意有
|MC|+|MB|=|MC|+|MA|=|AC|=r
又r>|BC|=2
∴点M的轨迹是以C(-1,0),B(1,0)为焦点的椭圆

∴a=![]() c=1
c=1
∴曲线F的方程为:
(2)反证法:假设直线l与椭圆F还有另一个交点![]() ,连接
,连接![]() C、
C、![]() B、
B、![]() A
A
∵点![]() 在l上,有|
在l上,有|![]() C|+|
C|+|![]() B|=|
B|=|![]() C|+|
C|+|![]() A|>|AC|=r
A|>|AC|=r
又点![]() 在F上,有 |
在F上,有 |![]() C|+|
C|+|![]() B|=r,两者矛盾
B|=r,两者矛盾
故假设不成立,原命题成立.
(3)∵r=4,故椭圆F方程为![]()
设点M(2cosθ,![]() sinθ)
sinθ)
则![]() =(2cosθ+1,
=(2cosθ+1,![]() sinθ),
sinθ),![]() =(2cosθ-1,
=(2cosθ-1,![]() sinθ),
sinθ),
∴![]() ·
·![]() =4cos2θ-1+3sin2θ=
=4cos2θ-1+3sin2θ=![]()
∴cos2θ=![]() ∴M(1,
∴M(1,![]() )
)
由(2)知l为椭圆F的切线,由
![]() ,当y>0时,有y=
,当y>0时,有y=![]()
∴![]() ∴kl=
∴kl=![]()
[由公式![]() 求kl不扣分(其中x1=1,y1=
求kl不扣分(其中x1=1,y1=![]() )]
)]
又kMC= 故tanα=
故tanα=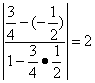 .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
 (2006•朝阳区二模)如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(2006•朝阳区二模)如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.| CE |
| CF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆C的方程为:x2+y2+x-6y+m=0,直线l的方程为:x+2y-3=0.
如图,已知圆C的方程为:x2+y2+x-6y+m=0,直线l的方程为:x+2y-3=0.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,已知椭圆D:
(2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,已知椭圆D:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.| q | p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com