设函数f(x)是定义在x∈[-1,1]上的偶函数,函数g(x)的图象与f(x)的图象关于直线x=1对称,且当x∈[2,3]时,g(x)=2a(x-2)-4(x-2)3
①求f(x)的解析式;
②是否存在正整数a,使f(x)的最大值为12?若存在求出a的值,若不存在说明理由.
【答案】
分析:(1)先设f(x)的图象上任意点(x,f(x)),求出它关于直线x=1的对称点的坐标,由题意给出x的范围,再代入g(x)的解析式化简,再由偶函数的关系式求出另外一部分的解析式,最后用分段函数的形式表示出来;
(2)先假设存在,由偶函数的性质确定研究的对象,再求出函数的导数和临界点,根据临界点与区间的关系分类讨论,由导数与函数的关系判断函数的单调性,并求出函数的最值,再由题意列出方程求出a的值.
解答:解:(1)设f(x)的图象上任意点(x,f(x)),
它关于直线x=1的对称点(2-x,f(x))在g(x)的图象上,
当x∈[-1,0]时,2-x∈[2,3],且g(x)=2a(x-2)-4(x-2)
3,
∴f(x)=g(2-x)=-2ax+4x
3,
当x∈(0,1]时,-x∈[-1,0),∴f(-x)=2ax-4x
3,
又∵f(x)是定义在x∈[-1,1]上的偶函数,
∴f(x)=2ax-4x
3,
则
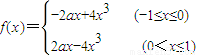
,
(2)假设存在正整数a,使函数f(x)的最大值为12,
又f(x)为偶函数,故只需研究函数f(x)=2ax-4x
3在x∈(0,1]的最大值
令f′(x)=2a-12x
2=0,得
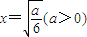
,
若
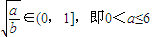
时:
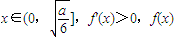
单调递增,
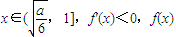
单调递减,
则

故此时不存在符合题意的a,
若

时,f′(x)>0在(0,1]上恒成立,
则f(x)在(0,1]上单调递增,
∴
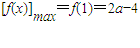
,
令2a-4=12,得a=8,
综上,存在a=8满足题意.
点评:本题考查了函数的对称性,奇偶性的综合应用,还考查了导数与函数性质之间的关系,涉及了分类讨论思想和存在性问题等,比较综合,属于中档题.

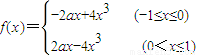 ,
,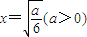 ,
,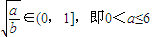 时:
时: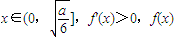 单调递增,
单调递增,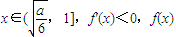 单调递减,
单调递减,
 时,f′(x)>0在(0,1]上恒成立,
时,f′(x)>0在(0,1]上恒成立,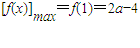 ,
,
