
| A、60种 | B、90种 |
| C、150种 | D、240种 |
| ||||
|
| C | 3 5 |


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
| A、f(x)的图象过原点 |
| B、f(x)的图象关于原点对称 |
| C、f(x)的图象关于y轴对称 |
| D、f(x)=x4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
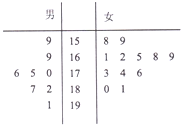 第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.
第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com