
分析 利用同角三角函数的基本关系求得sinα、cos(α+β)的值,再利用两角差的余弦公式求得cosβ=cos[(α+β)-α]的值.
解答 解:∵α,β∈(0,π),且cosα=$\frac{1}{7}$,
∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{4\sqrt{3}}{7}$,
∵sin(α+β)=$\frac{{5\sqrt{3}}}{14}$,
∴sinα>sin(α+β),
∴α+β为钝角,
∴cos(α+β)=-$\sqrt{{1-sin}^{2}(α+β)}$=-$\frac{11}{14}$,
则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-$\frac{11}{14}$•$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$•$\frac{4\sqrt{3}}{7}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查同角三角函数的基本关系、两角和差的余弦公式的应用,属于基础题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 中学成绩不优秀 | 中学成绩优秀 | 总计 | |
| 小学成绩优秀 | 5 | 20 | 25 |
| 小学成绩不优秀 | 10 | 5 | 15 |
| 合计 | 15 | 25 | 40 |
| A. | 在犯错误的概率不超过0.1的前提下,认为“小学成绩与中学成绩无关” | |
| B. | 在犯错误的概率不超过0.1的前提下,认为“小学成绩与中学成绩有关” | |
| C. | 在犯错误的概率不超过0.01的前提下,认为“小学成绩与中学成绩无关” | |
| D. | 在犯错误的概率不超过0.01的前提下,认为“小学成绩与中学成绩有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知f(x)=2sin(2x+$\frac{π}{3}$).
已知f(x)=2sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
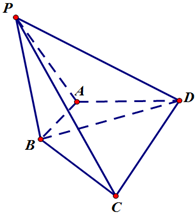 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-3i | B. | 3+i | C. | -$\sqrt{2}$+$\sqrt{2}$i | D. | $\sqrt{2}$+$\sqrt{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com