
分析 (I)ξ的所有可能取值有6,2,1,-2,分别求出相应的概率,由此能求出ξ的分布列.
(II)由ξ的分布列,能求出1件产品的平均利润.
(III)设技术革新后的三等品率为x,求出此时1件产品的平均利润为E(x)=4.76-x(0≤x≤0.29),由此能求出三等品率最多为1%.
解答 (满分12分)
解:(I)ξ的所有可能取值有6,2,1,-2,
$P(ξ=6)=\frac{252}{400}=0.63$,
$P(ξ=2)=\frac{100}{400}=0.25$,
$P(ξ=1)=\frac{40}{400}=0.1$,
$P(ξ=-2)=\frac{8}{400}=0.02$,
故ξ的分布列为:
| ξ | 6 | 2 | 1 | -2 |
| P | 0.63 | 0.25 | 0.1 | 0.02 |
点评 本题考查概率分布列的求法,考查产品的平均利润的求法,考查三等品率的求法,是中档题,解题时要认真审题,注意不等式性质的合理运用.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {2} | C. | {0,2} | D. | {0,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
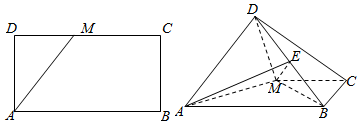
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com