练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （本小题满分14分）
    将一颗骰子先后抛掷2次，观察向上的点数，求：
    （Ⅰ）两数之和为5的概率；
    （Ⅱ）以第一次向上点数为横坐标x，第二次向上的点数为纵坐标y的点(x,y)在圆=15的内部的概率．
    解: 将一颗骰子先后抛掷2次，此问题中含有36个等可能基本事件       
    （I）记“两数之和为5”为事件A，则事件A中含有4个基本事件，
    所以P（A）=； 答：两数之和为5的概率为．              （6分）                          
    （II）基本事件总数为36，点（x，y）在圆x2+y2=15的内部记为事件C，则C包含8个事件，所以P（C）=．    答：点(x,y)在圆x2+y2=15的内部的概率为．（8分）
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    甲乙两个奥运会主办城市之间有7条网线并联，这7条网线能通过的信息量分别为l，1，2，2，2，3，3，现从中任选三条网线，设可通过的信息量为X，当可通过的信息量X≥6，则可保证信息通畅．
    （1）求线路信息通畅的概率；
    （2）求线路可通过的信息量X的分布列及期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    某大学毕业生响应国家号召，到某村参加村委会主任应聘考核。考核依次分为笔试、面
    试．试用共三轮进行，规定只有通过前一轮考核才能进入下一轮考核，否则将被淘汰，
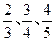    三轮考核都通过才能被正式录用。设该大学毕业生通过三轮考核的概率分别为， 且各轮考核通过与否相互独立。
    （Ⅰ）求该大学毕业生未进入第三轮考核的概率；
    （Ⅱ）设该大学毕业生在应聘考核中考核次数为ξ，求ξ的数学期望和方差。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分15分）
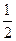    一次数学考试共有10道选择题，每道选择题都有4个选项，其中有且只有一个选项是正确的．设计试卷时，安排前n道题使考生都能得出正确答案，安排8-n道题，每题得出正确答案的概率为，安排最后两道题，每题得出正确答案的概率为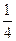，且每题答对与否相互独立，同时规定：每题选对得5分，不选或选错得0分．
    （1）当n=6时，
    ①分别求考生10道题全答对的概率和答对8道题的概率；
    ②问：考生答对几道题的概率最大，并求出最大值；
    （2）要使考生所得分数的期望不小于40分，求n的最小值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （文科做）
    设集合，，且满足, 若．
    (Ⅰ) 求b = c的概率；
    （Ⅱ）求方程有实根的概率

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了迎接2009年10月1日建国60周年，某城市为举办的大型庆典活动准备了四种保证安全的方案，列表如下：
    方案
    		A
    		B
    		C
    		D
    经费
    		300万元
    		400万元
    		500万元
    		600万元
    安全系数
    		0．6
    		0．7
    		0．8
    		0．9
    其中安全系数表示实施此方案能保证安全的系数，每种方案相互独立，每种方案既可独立用，又可以与其它方案合用，合用时，至少有一种方案就能保证整个活动的安全。
    （I）若总经费在1200万元内（含1200万元），如何组合实施方案可以使安全系数最高？
    （II）要保证安全系数不小于0．99，至少需要多少经费？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    甲乙两人进行相棋比赛,甲获胜的概率是0.4,两人下成和棋的概率是0.2,则甲不输的概率是(   )
    A．0.6B．0.8C．0.2D．0.4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    如图4，矩形ABCD，AB=2，BC=1，A，B两点关于坐标原点对称，在矩形ABCD内随机撒一把黄豆，落在曲线与轴所围成阴影部分的概率为     .
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知且E（）=10，D（）=6，则              .

    查看答案和解析>>

    同步练习册答案