
 的单调递增区间为[m,n]
的单调递增区间为[m,n] ,x求证x1<|x|<x2.
,x求证x1<|x|<x2. ,依题意,m,n是方程-4x2-2ax+4=0的两根,由此能够证明f(m)f(n)=-4.
,依题意,m,n是方程-4x2-2ax+4=0的两根,由此能够证明f(m)f(n)=-4. ,知n-m取最小值时,a=0,n=1,m=-1,由f(x)在[-1,1]是增函数,0<x1<x2<1,知
,知n-m取最小值时,a=0,n=1,m=-1,由f(x)在[-1,1]是增函数,0<x1<x2<1,知 >0,从而x∈(-1,1).由此入手,结合题设条件能够证明x1<|x|<x2.
>0,从而x∈(-1,1).由此入手,结合题设条件能够证明x1<|x|<x2. ,
, ,
,

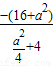 =-4.
=-4.
 ,
, >0,从而x∈(-1,1).
>0,从而x∈(-1,1). =
= =
= ,
,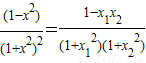 .
.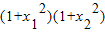 =
=
 ,
, =
= <
<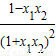 .
.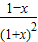 ,则g′(x)=
,则g′(x)= ,
,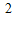 )<g(x1x2),得
)<g(x1x2),得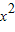 >x1x2>x
>x1x2>x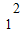 ,∴|x|>x1.
,∴|x|>x1. =
= ,及0<1-x
,及0<1-x <1-x1x2,
<1-x1x2, <
<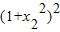 ,
, <1+
<1+ ,即|x|<x2,
,即|x|<x2,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试、理科数学(安徽卷) 题型:013
动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A的坐标是![]() ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区向是
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区向是
[0,1]
[1,7]
[7,12]
[0,1]和[7,12]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com