解:(1))|

+

|=(3+cosα,sinα)
∴
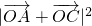
=9+6cosα+cos
2α+sin
2α=10+6cosα=13cosα=

∵α∈(0,π),∴α=

.(3分)
(2)∵cos<

,

>=
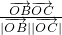
=

=sinα=

.(6分)
(3)∵

=(cosα-3,sinα),

=(cosα,sinα-3).(8分)
∴

•

=cos
2α-3cosα+sin
2α-3sinα=1-3(sinα+cosα)=-1
∴sinα+cosα=

(10分)
∴1+2sinαcosα=

.
∴sin2α=-

…(12分)
分析:(1)由已知中,A(3,0),C(cosα,sinα),我们可以求出向量

+

的坐标,进而根据|

+

|=

,我们可以代入向量坐标公式,易构造关于α的三角方程,根据α∈(0,π),解三角方程即可求出α的值;
(2)由已知中B(0,3),结合(1)中的结论,代入向量夹角公式,cos<

,

>=
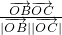
,即可求出

与

的夹角的余弦,进而得到

与

的夹角;
(3)根据A(3,0),B(0,3),C(cosα,sinα),由

•

=-1,我们易构造关于α的三角方程,化简后,即可得到sin2α的值.
点评:本题考查的知识点是平面向量的模,平面向量的夹角公式,平面向量的数量积,同角三角函数的基本关系,二倍角公式等,是三角函数与向量的综合应用,其中(1)的关键是确定向量

+

的坐标,(2)的关键是熟练掌握向量夹角公式,cos<

,

>=
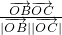
,(3)的关键是由已知条件构造关于α的三角函数方程.

 +
+ |=
|= ,且α∈(0,π),求α.
,且α∈(0,π),求α. 与
与 的夹角;
的夹角; •
• =-1,求sin2α的值.
=-1,求sin2α的值. +
+ |=(3+cosα,sinα)
|=(3+cosα,sinα)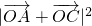 =9+6cosα+cos2α+sin2α=10+6cosα=13cosα=
=9+6cosα+cos2α+sin2α=10+6cosα=13cosα=
 .(3分)
.(3分) ,
, >=
>=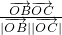 =
= =sinα=
=sinα= .(6分)
.(6分) =(cosα-3,sinα),
=(cosα-3,sinα), =(cosα,sinα-3).(8分)
=(cosα,sinα-3).(8分) •
• =cos2α-3cosα+sin2α-3sinα=1-3(sinα+cosα)=-1
=cos2α-3cosα+sin2α-3sinα=1-3(sinα+cosα)=-1 (10分)
(10分) .
. …(12分)
…(12分) +
+ 的坐标,进而根据|
的坐标,进而根据| +
+ |=
|= ,我们可以代入向量坐标公式,易构造关于α的三角方程,根据α∈(0,π),解三角方程即可求出α的值;
,我们可以代入向量坐标公式,易构造关于α的三角方程,根据α∈(0,π),解三角方程即可求出α的值; ,
, >=
>=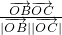 ,即可求出
,即可求出 与
与 的夹角的余弦,进而得到
的夹角的余弦,进而得到 与
与 的夹角;
的夹角; •
• =-1,我们易构造关于α的三角方程,化简后,即可得到sin2α的值.
=-1,我们易构造关于α的三角方程,化简后,即可得到sin2α的值. +
+ 的坐标,(2)的关键是熟练掌握向量夹角公式,cos<
的坐标,(2)的关键是熟练掌握向量夹角公式,cos< ,
, >=
>=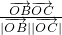 ,(3)的关键是由已知条件构造关于α的三角函数方程.
,(3)的关键是由已知条件构造关于α的三角函数方程. 
