
分析 (1)f利用二倍角余弦公式及变形,两角和的正弦公式化简解析式,由三角函数的周期公式求出(x)最小正周期;
(2)由正弦函数的最值求出f(x)的最大值;
(3)由正弦函数的增区间和整体思想求出f(x)单调递增区间.
解答 解:(1)由题意得,f(x)=$\sqrt{3}$cos2x+$\frac{1}{2}$sin2x
=$\frac{\sqrt{3}}{2}(1+cos2x)+\frac{1}{2}sin2x$=$sin(2x+\frac{π}{3})+\frac{\sqrt{3}}{2}$,
∴f(x)最小正周期T=$\frac{2π}{2}=π$;
(2)当$sin(2x+\frac{π}{3})=1$ 时,函数f(x)取到最大值是$1+\frac{\sqrt{3}}{2}$;
(3)由$-\frac{π}{2}+2kπ≤2x+\frac{π}{3}≤\frac{π}{2}+2kπ(k∈Z)$得,
$-\frac{5π}{12}+kπ≤x≤\frac{π}{12}+kπ(k∈Z)$,
∴f(x)单调递增区间是$[-\frac{5π}{12}+kπ,\frac{π}{12}+kπ](k∈Z)$.
点评 本题考查了二倍角余弦公式及变形,两角和的正弦公式,以及正弦函数的图象与性质,考查整体思想,化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
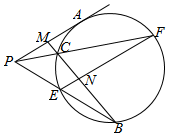 如图,PA是圆的切线,A是切点,M是PA的中点,过点M作圆的割线交圆于点C,B,连接PB,PC分别交圆于点E,F,EF与BC的交点为N.
如图,PA是圆的切线,A是切点,M是PA的中点,过点M作圆的割线交圆于点C,B,连接PB,PC分别交圆于点E,F,EF与BC的交点为N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在AB为直径的半圆O上取一点C,连接AC并延长与过B点的切线相交于点D,以C为切点作切线交AB的延长线于G,交BD于F.
如图,在AB为直径的半圆O上取一点C,连接AC并延长与过B点的切线相交于点D,以C为切点作切线交AB的延长线于G,交BD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
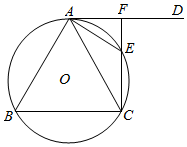 如图所示,△ABC内接于⊙O,AD是⊙O的切线,切点为A,∠DAC的平分线交⊙O于E,且满足AB⊥AE.
如图所示,△ABC内接于⊙O,AD是⊙O的切线,切点为A,∠DAC的平分线交⊙O于E,且满足AB⊥AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com