
分析 由已知求出cosα,进一步得到tanα,代入二倍角公式得答案.
解答 解:∵α为第二象限角,且sinα=$\frac{3}{5}$,
∴cosα=$-\sqrt{1-si{n}^{2}α}=-\sqrt{1-(\frac{3}{5})^{2}}=-\frac{4}{5}$,
则tanα=$\frac{sinα}{cosα}=-\frac{3}{4}$.
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×(-\frac{3}{4})}{1-(-\frac{3}{4})^{2}}$=$-\frac{24}{7}$.
故答案为:$-\frac{24}{7}$.
点评 本题考查三角函数中的恒等变换应用,考查了同角三角函数基本关系式及二倍角公式的应用,是基础题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
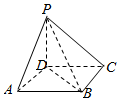 如图,四棱锥P-ABCD中,底面ABCD为矩形,AB=2AD,平面PDA⊥平面ABCD,平面PDC⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AB=2AD,平面PDA⊥平面ABCD,平面PDC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
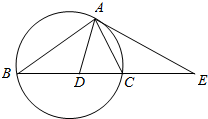 如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,AE=2BD=2.
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,AE=2BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com