
分析 构造函数f(x)=sinx-x+$\frac{x^3}{6}$,x∈(0,$\frac{π}{2}$).证明f(x)=sinx-x+$\frac{x^3}{6}$是单增函数,即可证明结论.
解答 解:令f(x)=sinx-x+$\frac{x^3}{6}$,x∈(0,$\frac{π}{2}$).f(0)=0.--(2分)
f′(x)=cosx-1+$\frac{1}{2}{x}^{2}$,f″(x)=-sinx+x.--(4分)
由三角不等式sinx<x,x∈(0,$\frac{π}{2}$),f″(x)>0.--(6分)
所以f′(x)是单调递增的,又f′(0)=0,
所以f′(x)>0恒成立,
所以f(x)=sinx-x+$\frac{x^3}{6}$是单增函数,
所以f(x)>f(0)=0--(8分)
即:sinx>x-$\frac{x^3}{6}$,x∈(0,$\frac{π}{2}$).--(10分)
点评 本题考查利用导数证明不等式,考查学生分析解决问题的能力,正确构造函数,确定函数的单调性是关键.


科目:高中数学 来源: 题型:解答题
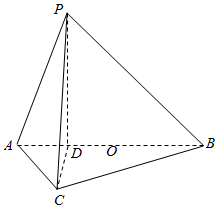 在直三棱锥P-ABC中,侧面PAB与底面ABC垂直,且PD垂直底面,PD=BD,△ACB是直角三角形,AD=$\frac{1}{3}$DB;BC=$\sqrt{3}$AC.
在直三棱锥P-ABC中,侧面PAB与底面ABC垂直,且PD垂直底面,PD=BD,△ACB是直角三角形,AD=$\frac{1}{3}$DB;BC=$\sqrt{3}$AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
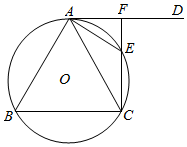 如图所示,△ABC内接于⊙O,AD是⊙O的切线,切点为A,∠DAC的平分线交⊙O于E,且满足AB⊥AE.
如图所示,△ABC内接于⊙O,AD是⊙O的切线,切点为A,∠DAC的平分线交⊙O于E,且满足AB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{{e}^{2}-1}{2e-1}$,+∞) | B. | (-∞,$\frac{{e}^{2}-1}{2e-1}$) | C. | (0,$\frac{{e}^{2}-1}{2e-1}$) | D. | {$\frac{{e}^{2}-1}{2e-1}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com