
 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$分析 (1)由同弧或等弧所对的圆周角相等,运用全等三角形的判定,可得△ABD≌△AFD,即可得到BD=DF;
(2)运用对应角相等,证得△DEF∽△FEA,可得EF2=ED•EA,设DE=x,求得EA,再由直角三角形DEF,运用勾股定理,解方程可得DE.
解答 解:(1) 由同弧或等弧所对的圆周角相等可得,
由同弧或等弧所对的圆周角相等可得,
∠ABD=∠AEC,∠DEC=∠DFC,
即有∠ABD=∠AFD,
又∠BAC的平分线交BC于点D,可得∠BAD=∠FAD,
且AD=AD,可得△ABD≌△AFD,
则DB=DF=$\sqrt{14}$;
(2)由同弧或等弧所对的圆周角相等可得,
∠DFE=∠DCE,∠DCE=∠BAE=∠EAC,
∴∠DFE=∠EAF,又∠DEF公用,
∴△DEF∽△FEA,
∴$\frac{EF}{EA}$=$\frac{DE}{FE}$,
∴EF2=ED•EA.
设DE=x,由AD=3,可得EA=3+x,
可得EF2=x(3+x),
在直角三角形DEF中,可得DE2+EF2=DF2,
即有x2+x(3+x)=14,
解得x=2(负的舍去).
则DE的长为2.
点评 本题考查圆的同弧或等弧所对的圆周角相等,三角形全等和相似的判定和性质、直角三角形的勾股定理的运用,考查推理和运算能力,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [2,+∞) | C. | $[-\frac{1}{2},2]$ | D. | $(-\frac{1}{2},2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a2+a3-a1,b2+b3-b1) | B. | (b2+b3-b1,a2+a3-a1) | ||
| C. | (a2+a3-2a1,b2+b3-2b1) | D. | (b2+b3-2b1,a2+a3-2a1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
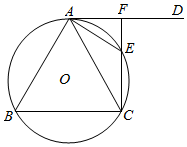 如图所示,△ABC内接于⊙O,AD是⊙O的切线,切点为A,∠DAC的平分线交⊙O于E,且满足AB⊥AE.
如图所示,△ABC内接于⊙O,AD是⊙O的切线,切点为A,∠DAC的平分线交⊙O于E,且满足AB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com