
| A. | (-∞,2] | B. | [2,+∞) | C. | $[-\frac{1}{2},2]$ | D. | $(-\frac{1}{2},2]$ |
分析 可看出该函数是由t=x2-ax+3a和$y=lo{g}_{\frac{1}{3}}t$复合而成的复合函数,这样根据二次函数、对数函数和复合函数的单调性及对数函数的定义域便可建立关于a的不等式组,解出a的取值范围即可.
解答 解:设y=f(x),令x2-ax+3a=t,则$y=lo{g}_{\frac{1}{3}}t$单调递减;
∵f(x)在[1,+∞)上单调递减;
∴t=x2-ax+3a在[1,+∞)上单调递增,且满足t>0;
∴$\left\{\begin{array}{l}{\frac{a}{2}≤1}\\{{1}^{2}-a•1+3a>0}\end{array}\right.$;
解得,$-\frac{1}{2}<a≤2$;
∴实数a的取值范围是$(-\frac{1}{2},2]$.
故选D.
点评 本题考查二次函数、对数函数和复合函数的单调性,以及复合函数的定义,对数函数的定义域.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y′=$\frac{\sqrt{3}}{2}$sin2x′ | B. | y′=2sin2x′ | C. | y′=$\frac{1}{2}$sin$\frac{2\sqrt{3}}{3}$x′ | D. | y′=$\sqrt{3}$sin2x′ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
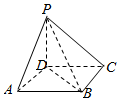 如图,四棱锥P-ABCD中,底面ABCD为矩形,AB=2AD,平面PDA⊥平面ABCD,平面PDC⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AB=2AD,平面PDA⊥平面ABCD,平面PDC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com