
分析 如图所示,y=g(x)=f(x)-1=$\left\{\begin{array}{l}{-(x-\frac{1}{2})^{2}+\frac{1}{4},0≤x≤\frac{1+\sqrt{5}}{2}}\\{(x-\frac{1}{2})^{2}-\frac{9}{4},\frac{1+\sqrt{5}}{2}<x<2}\end{array}\right.$,再利用f(x+2)=f(x),可得x∈[2,4]上的图象.由函数f(x)是R上的偶函数,可得g(x)也是R上的偶函数,结合图象即可得出零点个数.
解答 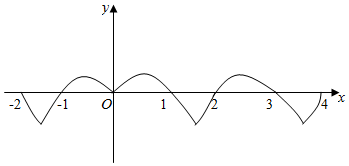 解:如图所示,y=g(x)=f(x)-1=$\left\{\begin{array}{l}{-(x-\frac{1}{2})^{2}+\frac{1}{4},0≤x≤\frac{1+\sqrt{5}}{2}}\\{(x-\frac{1}{2})^{2}-\frac{9}{4},\frac{1+\sqrt{5}}{2}<x<2}\end{array}\right.$,
解:如图所示,y=g(x)=f(x)-1=$\left\{\begin{array}{l}{-(x-\frac{1}{2})^{2}+\frac{1}{4},0≤x≤\frac{1+\sqrt{5}}{2}}\\{(x-\frac{1}{2})^{2}-\frac{9}{4},\frac{1+\sqrt{5}}{2}<x<2}\end{array}\right.$,
再利用f(x+2)=f(x),可得x∈[2,4]上的图象.
由函数f(x)是R上的偶函数,可得g(x)也是R上的偶函数,利用偶函数的性质可得x∈[-2,0)上的图象.
x∈[0,2)时,g(0)=g(1)=0,
x∈[2,4]时,g(2)=g(4)=g(0)=0,g(3)=g(1)=0.
x∈[-2,0)时,g(-2)=g(2)=0,g(-1)=g(1)=0.
指数可得:函数g(x)共有7个零点.
故答案为:7.
点评 本题考查了函数的奇偶性与周期性、绝对值函数的图象、二次函数的图象与性质,考查了数形结合方法、推理能力与计算能力,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
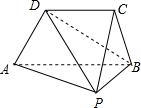 如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2
如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
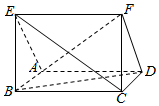 如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.
如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [2,+∞) | C. | $[-\frac{1}{2},2]$ | D. | $(-\frac{1}{2},2]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com