
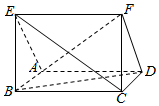
 如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.
如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.分析 (1)以A为原点,AB为x轴,AC为y轴,过A作平面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能证明AE⊥CF.
(2)求出平面AEF的法向量和平面AEF的一个法向量,由此能求出二面角A-EF-C的平面角的余弦值.
解答 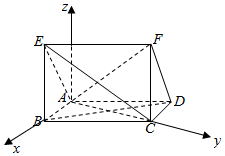 证明:(1)连接AC,设BC=2AB=2,则AC=$\sqrt{1+4-2×1×2×cos60°}$=$\sqrt{3}$,
证明:(1)连接AC,设BC=2AB=2,则AC=$\sqrt{1+4-2×1×2×cos60°}$=$\sqrt{3}$,
∵AB2+AC2=BC2,∴AB⊥AC,
∵四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD,
∴BE⊥平面ABCD,
以A为原点,AB为x轴,AC为y轴,过A作平面ABCD的垂线为z轴,建立空间直角坐标系,
则A(0,0,0),E(1,0,1),C(0,$\sqrt{3}$,0),F(-1,$\sqrt{3}$,1),
∴$\overrightarrow{AE}$=(1,0,1),$\overrightarrow{CF}$=(-1,0,1),
∴$\overrightarrow{AE}$•$\overrightarrow{CF}$=(1,0,1)•(-1,0,1)=0,
故AE⊥CF.
解:(2)A(0,0,0),E(1,0,1),C(0,$\sqrt{3}$,0),F(-1,$\sqrt{3}$,1),
所以$\overrightarrow{AE}$=(1,0,1),$\overrightarrow{AF}$=(-1,$\sqrt{3}$,1),=(1,-,1),$\overrightarrow{CF}$=(-1,0,1),$\overrightarrow{CE}$=(1,-$\sqrt{3}$,1),
设平面AEF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=x+z=0}\\{\overrightarrow{n}•\overrightarrow{AF}=-x+\sqrt{3}y+z=0}\end{array}\right.$,
取x=$\sqrt{3}$,得平面AEF的一个法向量为$\overrightarrow{n}$=($\sqrt{3}$,2,-$\sqrt{3}$),
设平面CEF的一个法向量为$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CE}=a-\sqrt{3}b+c=0}\\{\overrightarrow{m}•\overrightarrow{CF}=-a+c=0}\end{array}\right.$,取a=$\sqrt{3}$,则$\overrightarrow{m}$=($\sqrt{3}$,2,$\sqrt{3}$),
记二面角A-EF-C的平面角为α,由图可知,α为锐角,
则cosα=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{4}{10}$=$\frac{2}{5}$.
∴二面角A-EF-C的平面角的余弦值为$\frac{2}{5}$.
点评 本题考查线线垂直的证明、二面角余弦值的求解,考查考生的空间想象能力和运算求解能力.立体几何解答题主要围绕线面位置关系的证明以及空间角的计算展开,在线面位置关系中,垂直关系是核心,也是新课标高考命题的热点,空间角主要考查二面角,可利用传统法和向量法求解.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)<f(a)<f(c) | B. | f(b)<f(c)<f(a) | C. | f(a)<f(b)<f(c) | D. | f(c)<f(a)<f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com