
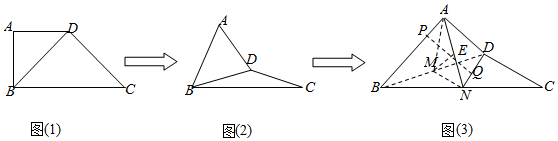
分析 (1)取BC的中点N,连接AN交BD于M,利用线面垂直的判定定理证明BD⊥平面AMN即可.
(2)得到∠AMN是二面角A-BD-C的平面角θ,根据线面角的定义得到∠ABH是AB与平面BCD所成角,结合三角形的边角关系进行求解即可.
(3)根据条件得到θ1+θ2=$\frac{π}{2}$,利用消元法转化为三角函数,利用三角函数的性质进行求解即可.
解答 证明:(1)取BC的中点N,连接AN交BD于M,
∵BC=2AD=2AB=2$\sqrt{2}$,
∴四边形ABND是正方形,
∴AM⊥BD,MN⊥BD,
∵AM∩MN=M,
∴BD⊥平面AMN,
∵ME?平面AMN,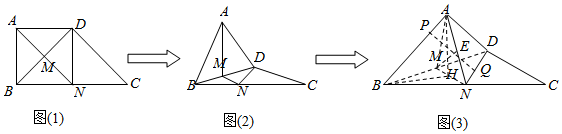
∴BD⊥ME,
解:(2)若θ=$\frac{π}{3}$,由(1)知∠AMN是二面角A-BD-C的平面角θ,
若θ=∠AMN=$\frac{π}{3}$,从而△AMN为等边三角形,
取MN的中点H,连接AH,
则AH⊥平面BCD,
连接BH,
则∠ABH是AB与平面BCD所成角,
则AB=$\sqrt{2}$,AM=MH=AN=1,
则AH=$\frac{\sqrt{3}}{2}$,
则sin∠ABH=$\frac{AH}{AB}$=$\frac{\frac{\sqrt{3}}{2}}{\sqrt{2}}$=$\frac{\sqrt{6}}{4}$.
解:(3)在BN线段取点R使得$\frac{AP}{PB}=\frac{NR}{RB}=\frac{NQ}{QD}=λ(λ∈R)$
从而易得PR∥AN且RQ∥BDA,θ1=∠PQR,θ2=∠QPR
另一方面,AM⊥BD,MN⊥BD,从而θ=∠AMN.
∵AM⊥BD,MN⊥BD,AM∩MN=M,
∴BD⊥AN,
∵PR∥AN,RQ∥BD,
∴∠PRQ=$\frac{π}{2}$,
从而有θ1+θ2=$\frac{π}{2}$,
则sinθ1+sinθ2=sinθ1+cosθ1=$\sqrt{2}$sin(θ1+$\frac{π}{4}$)∈(1,$\sqrt{2}$].
点评 本小题主要考查线面垂直的应用,线面角的求解,以及立体几何与三角函数的综合问题,考查空间想象能力、推理论证能力、运算求解能力等,考查化归与转化思想.综合性较强,有一定的难度.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
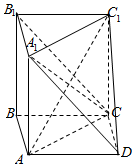 如图所示的几何体中,三棱柱ABC-A1B1C1为直三棱柱,ABCD为平行四边形,AD=2CD,∠ADC=60°.
如图所示的几何体中,三棱柱ABC-A1B1C1为直三棱柱,ABCD为平行四边形,AD=2CD,∠ADC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|4x<2x+1} | B. | {(x,y)|y=x-1} | C. | {y=x-1} | D. | {y|y=log2(-x2+2x+1)} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
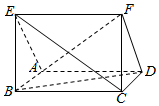 如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.
如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com