
分析 由方程f(x)=x2+m在(0,+∞)上两个解转化为m=f(x)-x2=$\frac{1}{3}$x3-x2-3x在(0,+∞)上两个解,构造函数h(x)=$\frac{1}{3}$x3-x2-3x,求函数的导数,利用导数研究函数的极值和取值范围即可.
解答 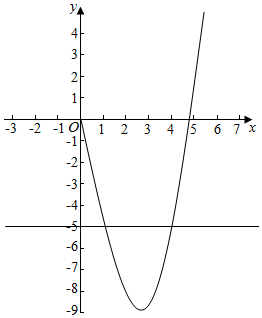 解:∵f(x)=$\frac{1}{3}$x3-3x,若方程f(x)=x2+m在(0,+∞)上两个解,
解:∵f(x)=$\frac{1}{3}$x3-3x,若方程f(x)=x2+m在(0,+∞)上两个解,
∴等价为m=f(x)-x2=$\frac{1}{3}$x3-x2-3x在(0,+∞)上两个解,
设h(x)=$\frac{1}{3}$x3-x2-3x,
则h′(x)=x2-2x-3,
由h′(x)>0得x>3或x<-1(舍),
由h′(x)<0得-1<x<3,即0<x<3,
即当x=3时,函数取得极小值h(3)=9-9-9=-9,
∵h(0)=0,
∴要使m=h(x)在(0,+∞)上有两个解,
则-9<m<0;
故答案为:-9<m<0
点评 本题主要考查函数与方程的应用,根据条件转化为两个函数的交点个数问题,利用条件构造函数,求函数的导数,利用导数研究函数的极值和取值范围是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)<f(a)<f(c) | B. | f(b)<f(c)<f(a) | C. | f(a)<f(b)<f(c) | D. | f(c)<f(a)<f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{5}$ | B. | 15 | C. | 6$\sqrt{5}$ | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y′=$\frac{\sqrt{3}}{2}$sin2x′ | B. | y′=2sin2x′ | C. | y′=$\frac{1}{2}$sin$\frac{2\sqrt{3}}{3}$x′ | D. | y′=$\sqrt{3}$sin2x′ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O内接四边形ABCD的两条对角线AC、BD交于点M,AP为⊙O的切线,∠BAP=∠BAC
如图,⊙O内接四边形ABCD的两条对角线AC、BD交于点M,AP为⊙O的切线,∠BAP=∠BAC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com