
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)根据分层抽样的定义和男生所占的比例列出方程,求出m的值,再由条件求出x、y的值;
(2)由(1)列出列联表,根据数据和公式求出K2的观测值,由表格和独立性检验即可得到答案.
解答 解:(1)设从高一年级男生中抽出m人,
则$\frac{m}{500}=\frac{45}{500+400}$,解得m=25,
∴x=25-20=5,y=20-18=2.(4分)
(2)2×2列联表如下:
| 男生 | 女生 | 总计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | 10 | 5 | 15 |
| 总计 | 25 | 20 | 45 |
点评 本题考查了分层抽样的定义,列联表、独立性检验的应用,考查计算能力.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=2x'\\ y=3y'\end{array}\right.$ | B. | .$\left\{\begin{array}{l}x=\frac{1}{2}x'\\ y=\frac{1}{3}y'\end{array}\right.$ | C. | .$\left\{\begin{array}{l}x=4x'\\ y=9y'\end{array}\right.$ | D. | .$\left\{\begin{array}{l}x=\frac{1}{4}x'\\ y=\frac{1}{9}y'\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-3x+1 | B. | y=|x+2| | C. | y=$\frac{4}{x}$ | D. | y=x2-4x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
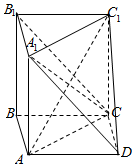 如图所示的几何体中,三棱柱ABC-A1B1C1为直三棱柱,ABCD为平行四边形,AD=2CD,∠ADC=60°.
如图所示的几何体中,三棱柱ABC-A1B1C1为直三棱柱,ABCD为平行四边形,AD=2CD,∠ADC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
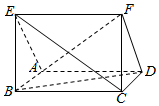 如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.
如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,四边形BEFD是矩形,且BE=BA,平面BEFD⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com