
分析 (1)设P(x,y),则M(x,2y),由点M在C1上,可得$\left\{\begin{array}{l}{x=2cosα}\\{2y=2+2sinα}\end{array}\right.$,化简即可得出C2的参数方程.
(2)圆C1的参数方程为:$\left\{\begin{array}{l}{x=2cosα}\\{y=2+2sinα}\end{array}\right.$(α为参数),化为普通方程,把ρ2=x2+y2,y=ρsinθ代入可得极坐标方程.C2的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=1+sinα}\end{array}\right.$(α为参数),化为普通方程,同理可得极坐标方程.射线$θ=\frac{π}{6}$与C1的交点A的极径ρ1=$4sin\frac{π}{6}$.射线$θ=\frac{π}{6}$与C2的交点B的极径ρ2=$\frac{8sin\frac{π}{6}}{1+3si{n}^{2}\frac{π}{6}}$,可得|AB|=|ρ1-ρ2|,又C1到BA的距离d=$2sin\frac{π}{3}$.即可得出${S}_{△{C}_{1}AB}$=$\frac{1}{2}$|BA|•d.
解答 解:(1)设P(x,y),则M(x,2y),∵点M在C1上,∴$\left\{\begin{array}{l}{x=2cosα}\\{2y=2+2sinα}\end{array}\right.$,即$\left\{\begin{array}{l}{x=2cosα}\\{y=a+sinα}\end{array}\right.$.
∴C2的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=1+sinα}\end{array}\right.$(α为参数).
(2)圆C1的参数方程为:$\left\{\begin{array}{l}{x=2cosα}\\{y=2+2sinα}\end{array}\right.$(α为参数),化为普通方程:x2+(y-2)2=4,展开为:x2+y2-4y=0.可得极坐标方程为:ρ2-4ρsinθ=0,即ρ=4sinθ.
C2的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=1+sinα}\end{array}\right.$(α为参数),化为普通方程:$\frac{{x}^{2}}{4}$+(y-1)2=1,展开为:x2+4y2-8y+3=0,
可得极坐标方程:ρ2(1+3sin2θ)-8ρsinθ=0.即ρ(1+3sin2θ)=8sinθ.
射线$θ=\frac{π}{6}$与C1的交点A的极径ρ1=$4sin\frac{π}{6}$=2.
射线$θ=\frac{π}{6}$与C2的交点B的极径ρ2=$\frac{8sin\frac{π}{6}}{1+3si{n}^{2}\frac{π}{6}}$=$\frac{16}{7}$.
∴|AB|=|ρ1-ρ2|=$\frac{2}{7}$,又C1到BA的距离d=$2sin\frac{π}{3}$=$\sqrt{3}$.
∴${S}_{△{C}_{1}AB}$=$\frac{1}{2}$|BA|•d=$\frac{1}{2}×\frac{2}{7}×\sqrt{3}$=$\frac{\sqrt{3}}{7}$.
点评 本题考查了参数方程化为普通方程、直角坐标方程化为极坐标方程、直线与曲线的交点、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E是边DC上的任意一点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E是边DC上的任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
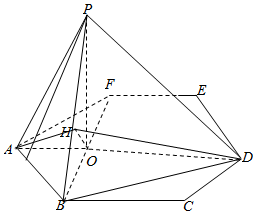 如图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.
如图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com