
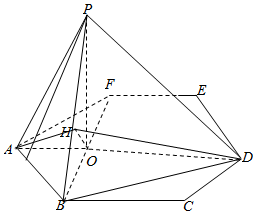
 如图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.
如图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.分析 (1)立体几何中证明直线与直线垂直,通常可用三垂线定理:因为P在平面ABC内的射影为O,所以PO⊥平面ABF,所以AO为PA在平面ABF内的射影;又因为O为BF中点,所以AO⊥BF,则PA⊥BF.
(2)二面角的度量关键在于作出它的平面角,常用的方法就是三垂线定理.由PO⊥平面ABF可得:AD⊥平面PBF,过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,所以∠AHD为所求二面角平面角.
解答 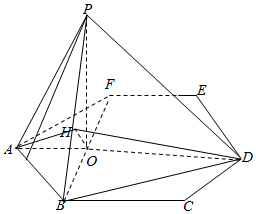 证明:(Ⅰ)在正六边形ABCDEF中,△ABF为等腰三角形,
证明:(Ⅰ)在正六边形ABCDEF中,△ABF为等腰三角形,
∵P在平面ABC内的射影为O,
∴PO⊥平面ABF,
∴AO为PA在平面ABF内的射影;
∵O为BF中点,
∴AO⊥BF,∴PA⊥BF.
解:(Ⅱ)∵PO⊥平面ABF,
∴平面PBF⊥平面ABC;
而O为BF中点,ABCDEF是正六边形,
∴A、O、D共线,且直线AD⊥BF,
则AD⊥平面PBF;
又∵正六边形ABCDEF的边长为1,
∴AO=$\frac{1}{2}$,DO=$\frac{3}{2}$,BO=$\frac{\sqrt{3}}{2}$,
过O在平面POB内作OH⊥PB于H,连AH、DH,
则AH⊥PB,DH⊥PB,所以∠AHD为所求二面角平面角,
在△AHO中,OH=$\frac{\sqrt{21}}{7}$,tan∠AHO=$\frac{AO}{OH}$=$\frac{\frac{1}{2}}{\frac{\sqrt{21}}{7}}$=$\frac{7}{2\sqrt{21}}$,
在△DHO中,tan∠DHO=$\frac{DO}{OH}$=$\frac{\frac{3}{2}}{\frac{\sqrt{21}}{7}}$=$\frac{\sqrt{21}}{2}$,
∴tan∠AHD=tan(∠AHO+∠DHO)=$\frac{\frac{7}{2\sqrt{21}}+\frac{\sqrt{21}}{2}}{1-\frac{7}{2\sqrt{21}}×\frac{\sqrt{21}}{2}}$=-$\frac{4×28}{3\sqrt{21}}$=-$\frac{16\sqrt{21}}{9}$,
∴cos∠AHD=-$\frac{3\sqrt{5457}}{1819}$.
∴面APB与面DPB所成二面角的大小的余弦值为-$\frac{3\sqrt{5457}}{1819}$.
点评 本小题主要考查棱锥的结构特征,二面角和线面关系等基本知识,同时考查空间想象能力和推理、运算能力


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
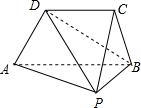 如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2
如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
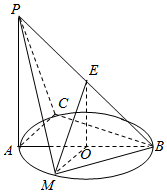 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com