
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)根据数学归纳法证明即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{-(x-1)[(a-1)x-1]}{{x}^{2}}$,
①1≤a<2时,$\frac{1}{a-1}$>1,
令f′(x)>0,解得:1<x<$\frac{1}{a-1}$,
令f′(x)<0,解得:x<1或x>$\frac{1}{a-1}$,
∴f(x)在(0,1)递减,在(1,$\frac{1}{a-1}$)递增,在($\frac{1}{a-1}$,+∞)递减;
②a=2时,f′(x)≤0,f(x)在(0,+∞)递减;
③a>2时,$\frac{1}{a-1}$<1,
令f′(x)>0,解得:$\frac{1}{a-1}$<x<1,
令f′(x)<0,解得:x>1或x<$\frac{1}{a-1}$,
∴f(x)在(0,$\frac{1}{a-1}$)递减,在($\frac{1}{a-1}$,1)递增,在(1,+∞)递减.
(2)证明:a=1时,f(x)=lnx+$\frac{1}{x}$,(x>0),
由(1)①得:f(x)在(0,1)递减,
∴f(x)<f(1)即lnx<1-$\frac{1}{x}$,
假设n=k时成立,
即$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k+1}$<ln(k+1)-$\frac{k}{3(k+1)}$成立,
则只需n=k+1时:
$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k+1}$+$\frac{1}{k+2}$<ln(k+1)-$\frac{k}{3(k+1)}$+$\frac{1}{k+2}$<ln(k+2)-$\frac{k+1}{3(k+2)}$即可,
∴只需证明ln$\frac{k+1}{k+2}$<$\frac{k}{3(k+1)}$-$\frac{1}{k+2}$-$\frac{k+1}{3(k+2)}$=-$\frac{3k+4}{3(k+1)(k+2)}$成立,
而ln$\frac{k+1}{k+2}$<1-$\frac{k+2}{k+1}$=-$\frac{1}{k+1}$,
-$\frac{1}{k+1}$-[-$\frac{3k+4}{3(k+1)(k+2)}$]=-$\frac{2}{3(k+1)(k+2)}$<0,
∴n=k+1时不等式成立,
故原结论成立.
点评 本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查不等式的证明,考查数学归纳法与分析法的运用,综合性强.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③④ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E是边DC上的任意一点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E是边DC上的任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
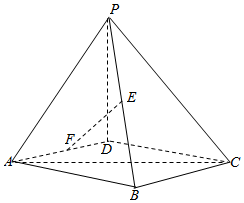 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD.
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
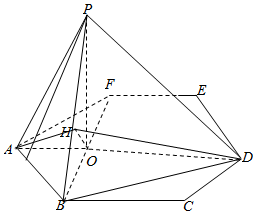 如图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.
如图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com