
| A. | ①③ | B. | ②③④ | C. | ①④ | D. | ①③④ |
分析 依题意,f′(x)=0在(0,+∞)上有二异根,作出f′(x)=$\frac{6lnx}{x}$-2的图象,对①②③④四个选项逐一分析即可确定答案.
解答  解:∵f(x)=3ln2x-2x,∴f′(x)=$\frac{6lnx}{x}$-2,
解:∵f(x)=3ln2x-2x,∴f′(x)=$\frac{6lnx}{x}$-2,
∵f(x)=3ln2x-2x有两个极值点x1,x2(x1<x2),
∴f′(x)=0在(0,+∞)上有二异根,
作出f′(x)=$\frac{6lnx}{x}$-2的图象,如图所示,则
①1<x1<3<x2成立;
②1<x1<x2<3,不成立;
f′(x1)=0,∴6lnx1=2x1,∴lnx1=$\frac{1}{3}$x1,
∴f(x1)=$\frac{1}{3}$x12-2x1=$\frac{1}{3}$(x1-3)2-3,
∵1<x1<2
∴-3<f(x1)<-$\frac{8}{3}$<-$\frac{5}{3}$,
∴③④成立.
故选:D.
点评 本题考查导数的综合应用,着重考查数形结合思想与等价转化思想、抽象思维与逻辑思维的综合应用,属于难题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 孵化鸭雏 | B. | 商品鸭饲养 | ||
| C. | 商品鸭收购、育肥、加工 | D. | 羽绒服加工生产体系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{2}{π}$ | D. | -$\frac{2}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
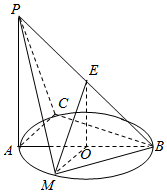 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com