
分析 法1:利用已知条件方程x+y+z=12的非负整数解,得出x,y,z的取值范围,列出所有的可能即可.
法2:利用插板法分成三组,利用组合进行求解.
解答 解:根据已知条件
∵x+y+z=12,且x、y、z∈N,
∴0≤x≤12,0≤y≤12,0≤z≤12,当x,y确定后z值也确定,其中z=12-x-y
列出所有的可能:
当x=0时,y+z=12,则y可以取0,1,2,3,4,5,6,7,8,9,10,11,12共13种情况;
当x=1时,y+z=11,y可以,0,1,2,3,4,5,6,7,8,9,10,11共12种情况;
当x=2时,y+z=10,y可以,0,1,2,3,4,5,6,7,8,9,10,共,11种情况;
当x=3时,y+z=9,y可以,0,1,2,3,4,5,6,7,8,9,共,10种情况;
当x=4时,y+z=8,y可以,0,1,2,3,4,5,6,7,8,共9种情况;
当x=5时,y+z=7,y可以,0,1,2,3,4,5,6,7,共8种情况;
当x=6时,y+z=6,y可以,0,1,2,3,4,5,6,共7种情况;
当x=7时,y+z=5,y可以,0,1,2,3,4,5,共6种情况;
当x=8时,y+z=4,y可以,0,1,2,3,4共5种情况;
当x=9时,y+z=3,y可以,0,1,2,3,共4种情况;
当x=10时,y+z=2,y可以,0,1,2,共3种情况;
当x=11时,y+z=1,y可以,0,1,共2种情况;
当x=12时,y+z=0,y可以,0,共1种情况;
所以共有13+12+11+10+9+8+7+6+5+4+3+2+1=91组.
方法2:插板法,将12看成12个1,12个1中间有14个空,从14个空中选两个进行插板,
插板之间1的个数即为该数对应的数值,
则共有C${\;}_{14}^{2}$=$\frac{14×13}{2}$=91,
△1△1△1△1△1△1△1△1△1△1△1△1△,
比如隔板插个如图所示△1△1△1↑1△1△1↑1△1△1△1△1△1△,
此时第一组x=3,第二组y=3,第三组z=6
故答案为:91.
点评 本题主要考查三元一次方程根的个数的求解,利用列举法或插板法分成三组是解决本题的关键.其中使用插板法比较简单.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
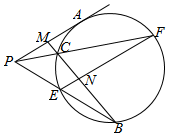 如图,PA是圆的切线,A是切点,M是PA的中点,过点M作圆的割线交圆于点C,B,连接PB,PC分别交圆于点E,F,EF与BC的交点为N.
如图,PA是圆的切线,A是切点,M是PA的中点,过点M作圆的割线交圆于点C,B,连接PB,PC分别交圆于点E,F,EF与BC的交点为N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com