
分析 (1)构造辅助函数h(x)=lnx-aex,求导,当a≤0和a>0,h′(x)的符号,根据极值的定义即可判断y=f(x)-ag(x)极值点的个数;
(2)由题意可知,将不等式转化成2ex-exx3>2构造辅助函数,求导,由x∈(0,1)时-ex<0,x+1>0;根据二次函数性质,判断函数k(x)的单调区间,求得函数的最大值,即可证明2ex-exx3>2,可得g(x)>$\frac{2}{2-{x}^{3}}$.
解答 解:(1)令h(x)=lnx-aex,
h′(x)=$\frac{1}{x}$-aex,
当a≤0时,h′(x)=$\frac{1}{x}$-aex>0,此时函数无极值点.…(2分)
当a>0时,令,h′(x)=$\frac{1}{x}$-aex=0,则$\frac{1}{x}$=aex,
显然?x0>0,使得$\frac{1}{{x}_{0}}$=$a{e}^{{x}_{0}}$,
当0<x<x0时,$\frac{1}{x}$>aex,即h′(x)>0,
当x>x0时,$\frac{1}{x}$<aex,即h′(x)<0,
此时函数有唯一极大值点,无极小值点.…(5分)
(2)证明:要证g(x)>$\frac{2}{2-{x}^{3}}$,即证2ex-exx3>2;…(6分)
令k(x)=2ex-exx3,
∴k′(x)=ex(-x3-3x2+2)=-ex(x3+3x2-2)=-ex(x+1)(x2+2x-2),…(7分)
故当x∈(0,1)时-ex<0,x+1>0;
令P(x)=x2+2x-2=0.则x=±$\sqrt{3}$-1(负值舍去)
故当x∈(0,$\sqrt{3}$-1)时,P(x)=x2+2x-2<0,故k′(x)=-ex(x+1)(x2+2x-2)>0,
即k(x)在(0,$\sqrt{3}$-1)上单调递增;…(9分)
当x∈($\sqrt{3}$-1,1)时,P(x)=x2+2x-2>0,
故k′(x)=-ex(x+1)(x2+2x-2)<0,
即k(x)在($\sqrt{3}$-1,1)上单调递减;
∵k(0)=2,k(1)=e,
故当x∈(0,1)时,k(x)>k(0)=2 即2ex-exx3>2,
故结论成立…(12分)
点评 本题考查利用导数研究函数的单调性、极值及不等式的证明,具体涉及到导数的性质、函数增减区间的判断、极值的计算和不等式性质的应用,解题时要认真审题,仔细解答,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
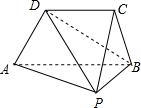 如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2
如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
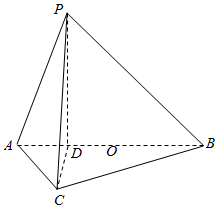 在直三棱锥P-ABC中,侧面PAB与底面ABC垂直,且PD垂直底面,PD=BD,△ACB是直角三角形,AD=$\frac{1}{3}$DB;BC=$\sqrt{3}$AC.
在直三棱锥P-ABC中,侧面PAB与底面ABC垂直,且PD垂直底面,PD=BD,△ACB是直角三角形,AD=$\frac{1}{3}$DB;BC=$\sqrt{3}$AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com