
| A. | -$\frac{1}{2}$ | B. | -1 | C. | 0 | D. | 1 |
分析 由f(x)=3x-4x3,知f′(x)=3-12x2,令f′(x)=3-12x2=0,得x=±$\frac{1}{2}$.由此能求出函数f(x)=3x-4x3,x∈[-1,0]的最小值.
解答 解:∵f(x)=3x-4x3,
∴f′(x)=3-12x2,
令f′(x)=3-12x2=0,
得x=±$\frac{1}{2}$.
∵x=$\frac{1}{2}$∉[-1,0],
∴x=$\frac{1}{2}$(舍).
∵f(0)=0,f(-$\frac{1}{2}$)=-$\frac{3}{2}$-4×(-$\frac{1}{2}$)3=-1,f(-1)=-3+4=1.
∴函数f(x)=3x-4x3,x∈[-1,0]的最小值是-1.
故选:B.
点评 本题考查函数的最小值的求法,是基础题,解题时要认真审题,仔细解答.如本题解答中没有研究单调性,于课本例题解答步骤不同,但在最值一定是在极值与端点值取到这一规律下,这一解答方式就规避了单调性的讨论,使得运算量降低,解题时可参考技巧降低解题难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
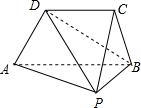 如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2
如图,四棱锥P-ABCD,DC∥AB,PB⊥AB,平面PAB⊥平面ABCD,AD=DC=CB=1,AB=BP=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{2}$] | B. | [0,$\frac{1}{4}$) | C. | (0,$\frac{1}{2}$] | D. | (0,$\frac{1}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [2,+∞) | C. | $[-\frac{1}{2},2]$ | D. | $(-\frac{1}{2},2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
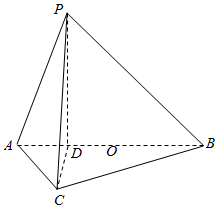 在直三棱锥P-ABC中,侧面PAB与底面ABC垂直,且PD垂直底面,PD=BD,△ACB是直角三角形,AD=$\frac{1}{3}$DB;BC=$\sqrt{3}$AC.
在直三棱锥P-ABC中,侧面PAB与底面ABC垂直,且PD垂直底面,PD=BD,△ACB是直角三角形,AD=$\frac{1}{3}$DB;BC=$\sqrt{3}$AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com