
分析 (Ⅰ)求出导数,利用曲线y=f(x)在点(1,f(1))处的切线方程为8x-2y-3=0,建立方程求a,b的值;
(Ⅱ)确定a>4且x1+x2=a,x1x2=a,化简f(x1)+f(x2),构造函数,确定函数的单调性,即可证明结论.
解答 解:(Ⅰ)根据题意可求得切点(1,2.5),f′(x)=$\frac{a}{x}$+x(1-b)
∴f(1)=0.5+1-b=2.5,f′(1)=a+1+1-b=4,解得a=1,b=-1----------(4分)
(Ⅱ)证明:∵b=a+1,∴f(x)=alnx+$\frac{1}{2}$x2-ax,则f′(x)=$\frac{{x}^{2}-ax+a}{x}$,
根据题意可得x2-ax+a=0在(0,+∞)上有两个不同的根x1,x2,
∴$\left\{\begin{array}{l}{\frac{a}{2}>0}\\{{a}^{2}-4a>0}\\{a>0}\end{array}\right.$解得a>4且x1+x2=a,x1x2=a,---------------(8分)
∴f(x1)+f(x2)=alnx1x2+$\frac{1}{2}$(x12+x22)-a(x1+x2)=alna-$\frac{1}{2}$a2-a.
令g(x)=xlnx=$\frac{1}{2}$x2-x(x>4),则g′(x)=lnx-x,
令h(x)=lnx-x,则当x>4时,h′(x)=$\frac{1}{x}$-1<0,∴h(x)在(4,+∞)上为减函数,
即h(x)<h(4)=ln4-4<0,
∴g(x)在(4,+∞)上为减函数,即g(x)<g(4)=8ln2-12,
∴f(x1)+f(x2)<8ln2-12------------------(12分)
点评 本题考查导数的综合应用:求单调区间和求极值,考查二次方程的韦达定理及运用,考查构造函数应用导数证明不等式,考查运算和逻辑推理能力,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | y′=$\frac{\sqrt{3}}{2}$sin2x′ | B. | y′=2sin2x′ | C. | y′=$\frac{1}{2}$sin$\frac{2\sqrt{3}}{3}$x′ | D. | y′=$\sqrt{3}$sin2x′ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
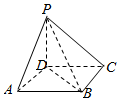 如图,四棱锥P-ABCD中,底面ABCD为矩形,AB=2AD,平面PDA⊥平面ABCD,平面PDC⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AB=2AD,平面PDA⊥平面ABCD,平面PDC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O内接四边形ABCD的两条对角线AC、BD交于点M,AP为⊙O的切线,∠BAP=∠BAC
如图,⊙O内接四边形ABCD的两条对角线AC、BD交于点M,AP为⊙O的切线,∠BAP=∠BAC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
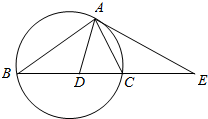 如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,AE=2BD=2.
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,AE=2BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com