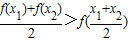解:(类型A)(1)f(x)=x
3+ax
2+x+1∴f'(x)=3x
2+2ax+1
当a
2≤3时,即

时,△≤0,f'(x)≥0,f(x)在R上递增.
当a
2>3时,即

或
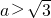
时,△>0,f'(x)=0求得两根为
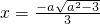
即f(x)在
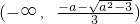
,
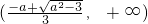
上递增,在

递减.
(2)f'(x)=3x
2+2ax+1≤0在

恒成立.
即

在

恒成立.
可知

在

上为减函数,在
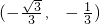
上为增函数.
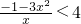
.
所以a≥2.a的取值范围是[2,+∞).
(类型B)(1)f(x)=x
3-ax+1∴f'(x)=3x
2-a
当a≤0时,f'(x)≥0,f(x)在R上递增.
当a>0时,f'(x)=0求得两根为x=±

即f(x)在(-∞,
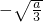
),(

,+∞)上递增,在(
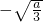
,

)递减.
(2)f'(x)=3x
2-a≤0在

恒成立.
即a≥3x
2在

恒成立.
可知3x
2在(-

,

)上为减函数,
所以a≥

.a的取值范围是[

,+∞).
分析:(类型A)(1)求出函数f(x)=x
3+ax
2+x+1,对参数a的范围进行讨论得出函数的单调区间.
(2)设函数f(x)在区间

内是减函数,即导数在在区间

内恒小于0由二次函数的性质转化出关于参数的不等式,解出a的取值范围.
(类型B))(1)求出函数f(x)=x
3-ax+1,对参数a的范围进行讨论得出函数的单调区间;
(2)先由函数求导,再由“函数f(x)在区间

内是减函数”转化为“f'(x)=3x
2-a≤0在

恒成立”,进一步转化为最值问题:3x
2≤a在

恒成立,求得函数的最值即可.
点评:本题考查利用导数研究函数的单调性,求解本题的关键是正确求出函数的导数,对于第一问要注意到参数的取值范围对导数的符号有影响故需要对参数分类讨论,而第二问中关键是把函数是减函数的性质转化为函数恒成立的问题,转化思想在高中数学在应用很广泛.

 内是减函数,求a的取值范围.
内是减函数,求a的取值范围. 内是减函数,求a的取值范围.
内是减函数,求a的取值范围. 时,△≤0,f'(x)≥0,f(x)在R上递增.
时,△≤0,f'(x)≥0,f(x)在R上递增. 或
或 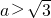 时,△>0,f'(x)=0求得两根为
时,△>0,f'(x)=0求得两根为 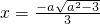
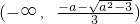 ,
,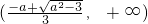 上递增,在
上递增,在  递减.
递减. 恒成立.
恒成立. 在
在  恒成立.
恒成立. 在
在  上为减函数,在
上为减函数,在 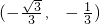 上为增函数.
上为增函数. 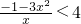 .
.
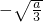 ),(
),( ,+∞)上递增,在(
,+∞)上递增,在(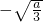 ,
, )递减.
)递减. 恒成立.
恒成立. 恒成立.
恒成立. ,
, )上为减函数,
)上为减函数, .a的取值范围是[
.a的取值范围是[ ,+∞).
,+∞). 内是减函数,即导数在在区间
内是减函数,即导数在在区间 内恒小于0由二次函数的性质转化出关于参数的不等式,解出a的取值范围.
内恒小于0由二次函数的性质转化出关于参数的不等式,解出a的取值范围. 内是减函数”转化为“f'(x)=3x2-a≤0在
内是减函数”转化为“f'(x)=3x2-a≤0在  恒成立”,进一步转化为最值问题:3x2≤a在
恒成立”,进一步转化为最值问题:3x2≤a在  恒成立,求得函数的最值即可.
恒成立,求得函数的最值即可.

 阅读快车系列答案
阅读快车系列答案 ,f(x)的导函数是f′(x),对任意两个不相等的正数x1,x2,证明:
,f(x)的导函数是f′(x),对任意两个不相等的正数x1,x2,证明: