
设数列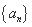 的前
的前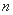 项和为
项和为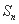 ,并且满足
,并且满足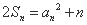 ,
,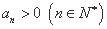 .
.
(Ⅰ) 求 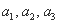 ;
;
(Ⅱ)猜想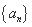 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
解:分别令n=1,2,3,得
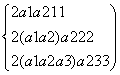
∵an>0,∴a1=1,a2=2,a3=3.
(2)解 猜想:an=n, 由2Sn=a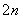 +n, ①
+n, ①
可知,当n≥2时,2Sn-1=a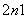 +(n-1), ②
+(n-1), ②
①-②,得2an=a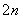 -a
-a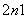 +1,即a
+1,即a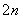 =2an+a
=2an+a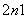 -1. (ⅰ)当n=2时,a
-1. (ⅰ)当n=2时,a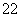 =2a2+12-1,∵a2>0,∴a2=2;
=2a2+12-1,∵a2>0,∴a2=2;
(ⅱ)假设当n=k(k≥2)时,ak=k.
那么当n=k+1时,
[ak+1-(k+1)][ak+1+(k-1)]=0,
∵ak+1>0,k≥2,∴ak+1+(k-1)>0,
∴ak+1=k+1.
这就是说,当n=k+1时也成立,
∴an=n(n≥2).显然n=1时,也适合.
综合(1)(2)可知对于n∈N*,an=n都成立。


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
由下表可得回归直线方程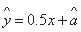 ,据此模型预报身高为
,据此模型预报身高为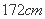 的男生的体重大约为( )
的男生的体重大约为( )
A.69.5 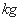 B.70
B.70 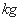 C.70.5
C.70.5 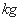 D.71
D.71 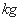
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com