
科目:高中数学 来源: 题型:
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
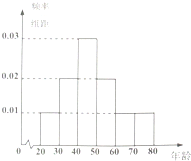 “行通济”是广东佛山一带在元宵节期间举行的游玩祈福活动,每到这一天,家家户户都会扶老携幼,自清晨到夜幕,举着风车、摇着风铃、拎着生菜浩浩荡荡地由北到南走过通济桥,祈求来年平平安安、顺顺利利.为了了解不同年龄层次的人对这一传统习俗的参与度,现随机抽取年龄在20~80岁之间的60人,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80)绘制频率分布直方图如图所示,其中参与了2014年“行通济”活动的人数如下表.若规定年龄分布在[20,60)岁的为“中青年人”,60岁以上(含60岁)为“老年人”.
“行通济”是广东佛山一带在元宵节期间举行的游玩祈福活动,每到这一天,家家户户都会扶老携幼,自清晨到夜幕,举着风车、摇着风铃、拎着生菜浩浩荡荡地由北到南走过通济桥,祈求来年平平安安、顺顺利利.为了了解不同年龄层次的人对这一传统习俗的参与度,现随机抽取年龄在20~80岁之间的60人,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80)绘制频率分布直方图如图所示,其中参与了2014年“行通济”活动的人数如下表.若规定年龄分布在[20,60)岁的为“中青年人”,60岁以上(含60岁)为“老年人”.| 年龄(岁) | 参与人数 |
| [20,30) | 3 |
| [30,40) | 2 |
| [40,50) | 3 |
| [50,60) | 4 |
| [60,70) | 5 |
| [70,80] | 3 |
| “老年人”人数 | “中青年人”人数 | 合计 | |
| 有参与 | |||
| 没有参与 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com