
分析 (Ⅰ)将圆的一般式方程化为标准式,求出圆心坐标和半径,由题意和点与圆的位置关系列出不等式组,求出k的取值范围;
(Ⅱ)由题意和圆的性质判断出P1、P2在以AB为直径的圆上,将k=$\frac{\sqrt{21}}{2}$代入求出圆C的方程,求出在以AB为直径的圆的方程,两圆的方程相减求出公共弦P1P2的方程,由点到直线的距离公式求出O到直线P1P2的距离,由弦长公式求出|P1P2|的值.
解答 解:(Ⅰ)圆C的标准方程是(x-k)2+(y+1)2=4k2-14,
∵过B(1,0)点至少能作一条直线与圆C相切,
∴B点在圆C外或在圆周上,则$\left\{\begin{array}{l}{1+{k}^{2}-2k+1≥4{k}^{2}-14}\\{4{k}^{2}-14>0}\end{array}\right.$,
解得$-\frac{8}{3}≤k<-\frac{\sqrt{14}}{2}$或$\frac{\sqrt{14}}{2}<k≤2$;
(Ⅱ)∵∠APiB=90°(i=1,2),
∴P1,P2在以AB为直径的圆上,
∵P1,P2在圆C上,
∴P1P2是两圆的公共弦,
当k=$\frac{\sqrt{21}}{2}$时,圆C的方程为:$(x-\frac{\sqrt{21}}{2})^{2}+(y+1)^{2}=7$,
即${x}^{2}+{y}^{2}-\sqrt{21}x+2y-\frac{3}{4}=0$,
以AB为直径的圆的方程是:x2+y2=1,
两圆方程相减得,公共弦所在的直线方程为$\sqrt{21}x-2y-\frac{1}{4}=0$,
∴O到直线P1P2的距离d=$\frac{\frac{1}{4}}{\sqrt{21+4}}$=$\frac{1}{20}$,
∴|P1P2|=2$\sqrt{1-(\frac{1}{20})^{2}}$=2×$\frac{\sqrt{399}}{20}$=$\frac{\sqrt{399}}{10}$.
点评 本题考查了点、直线、圆与圆的位置关系,点到直线的距离公式,弦长公式,以及配方法的应用,考查化简、计算能力.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(β)<g(μ)<g(α)<g(λ) | B. | g(μ)<g(β)<g(λ)<g(α) | C. | g(α)<g(λ)<g(μ)<g(β) | D. | g(β)<g(μ)<g(λ)<g(α) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
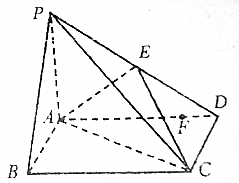 已知四棱锥P-ABCD中,PA⊥面ABCD,ABCD为矩形且PA=AB=2,AD=4,E为PD中点.
已知四棱锥P-ABCD中,PA⊥面ABCD,ABCD为矩形且PA=AB=2,AD=4,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com