
对于给定的大于1的正整数n,设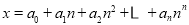 ,其中
,其中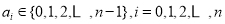 ,且
,且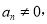 记满足条件的所有x的和为
记满足条件的所有x的和为 ,
,
(1)求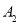 (2)设
(2)设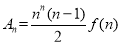 ,求
,求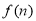
(1)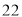 .(2)
.(2)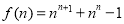
【解析】
试题分析:(1)实质为读题:当 时,
时, ,
,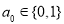 ,
,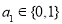 ,
,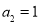 ,所以
,所以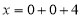 ,
,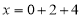 ,
,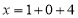 ,
,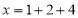 ,
,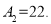
(2)问题实质为统计出现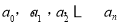 的次数,
的次数,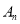 中所有含
中所有含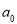 项的和为
项的和为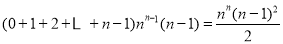 ;同理,
;同理,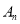 中所有含
中所有含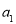 项的和为
项的和为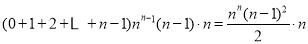 ;
;
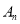 中所有含
中所有含 项的和为
项的和为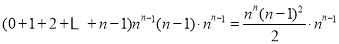 ;而
;而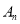 中所有含
中所有含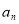 项的和为
项的和为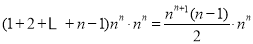 ;
;
所以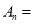
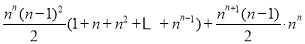 ;
;
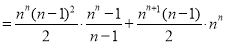
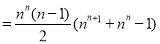 ,
,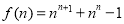
试题解析:(1)当 时,
时, ,
,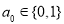 ,
,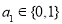 ,
,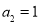 ,
,
故满足条件的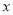 共有
共有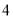 个,
个,
分别为: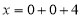 ,
,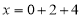 ,
,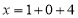 ,
,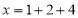 ,
,
它们的和是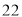 . 4分
. 4分
(2)由题意得,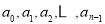 各有
各有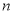 种取法;
种取法;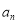 有
有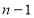 种取法,
种取法,
由分步计数原理可得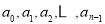 的不同取法共有
的不同取法共有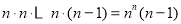 ,
,
即满足条件的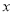 共有
共有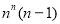 个, 6分
个, 6分
当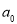 分别取
分别取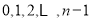 时,
时,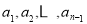 各有
各有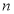 种取法,
种取法,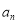 有
有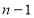 种取法,
种取法,
故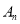 中所有含
中所有含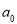 项的和为
项的和为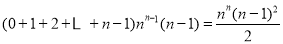 ;
;
同理,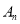 中所有含
中所有含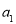 项的和为
项的和为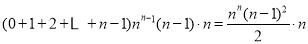 ;
;
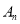 中所有含
中所有含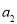 项的和为
项的和为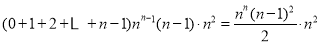 ;
;
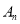 中所有含
中所有含 项的和为
项的和为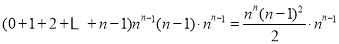 ;
;
当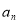 分别取
分别取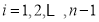 时,
时,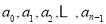 各有
各有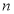 种取法,
种取法,
故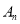 中所有含
中所有含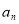 项的和为
项的和为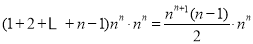 ;
;
所以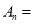
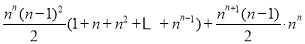 ;
;
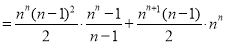
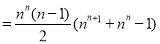
故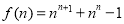 . 10分
. 10分
考点:分布计算原理
考点分析: 考点1:等比数列 试题属性

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源:2014-2015学年江苏省扬州市高三上学期期末理科数学试卷(解析版) 题型:解答题
已知数列{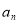 }中,
}中,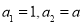 ,且
,且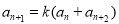 对任意正整数都成立,数列{
对任意正整数都成立,数列{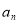 }的前n项和为Sn。
}的前n项和为Sn。
(1)若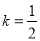 ,且
,且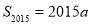 ,求a;
,求a;
(2)是否存在实数k,使数列{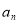 }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项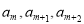 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若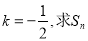 。
。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分14分)在平面直角坐标系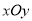 中,角
中,角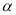 的终边经过点
的终边经过点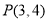 .
.
(1)求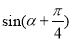 的值;
的值;
(2)若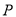 关于
关于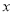 轴的对称点为
轴的对称点为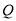 ,求
,求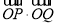 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省苏州市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
已知数列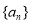 中
中
 .
.
(1)是否存在实数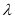 ,使数列
,使数列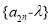 是等比数列?若存在,求
是等比数列?若存在,求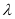 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若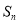 是数列
是数列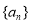 的前
的前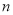 项和,求满足
项和,求满足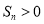 的所有正整数
的所有正整数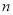 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com