
| A. | 2026 | B. | 2046 | C. | 1024 | D. | 1022 |
分析 由题意,及对数的换底公式知,a1•a2•a3…an=log2(n+2),由此知,劣数+2必为2的整数次幂,由此易得出劣数表达式,此区间(1,2010)内所有劣数的和是一个数列求和问题,由此计算出值选出正确答案.
解答 解:由题意an=log(n+1)(n+2),(n∈N*),若称使乘积a1•a2•a3…an为整数的数n为劣数且a1•a2•a3…an=log2(n+2)
故劣数n=2k-2,故最小的劣数为2=22-2,令n=2k-2<2010,
由于210-2=1022,211-2=2046
故最大的劣数为210-2,
∴(1,2010)内所有劣数的和为22-2+23-2+24-2+…+210-2=$\frac{{2}^{2}(1-{2}^{9})}{1-2}$-18=211-22=2026.
故选:A.
点评 本题考查数列的求和,正确理解劣数定义,找出区间(1,2010)内所有劣数,以及熟练掌握数列求和的技巧分组求和是求解本题的关键,本题中难点是理解劣数的定义,由此定义得出劣数的结构,将求和的问题转化为数列求和的问题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
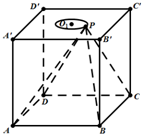 正方体ABCD-A1B1C1D1的棱长为6,半径为$\sqrt{6}$的圆O1在平面A1B1C1D1内,其圆心O1为正方形A1B1C1D1的中心,P为圆O1上的一个动点,则多面体PABCD的外接球的半径为$\sqrt{22}$.
正方体ABCD-A1B1C1D1的棱长为6,半径为$\sqrt{6}$的圆O1在平面A1B1C1D1内,其圆心O1为正方形A1B1C1D1的中心,P为圆O1上的一个动点,则多面体PABCD的外接球的半径为$\sqrt{22}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com