
分析 由已知得公共项构成的新数列{cn}是以c1=17为首项,d=28为公差的等差数列,从而cn=28n-11,求出a200=797,b200=1396,由cn=28n-11≤797,得到公共项28项,由此能求出公共项的总和.
解答 解:等差数列{an}:1,5,9,13,17,21,25,29,33,37,41,45,…
等差数列{bn}:3,10,17,24,31,38,45,…
∴公共项构成的新数列{cn}是以c1=17为首项,d=45-17=28为公差的等差数列,
∴cn=17+(n-1)×28=28n-11.
an=1+(n-1)(5-1)=4n-3,bn=3+(n-1)(10-3)=7n-4,
∴a200=4×200-3=797,b200=7×200-4=1396,
∴cn=28n-11≤797,解得n≤28$\frac{6}{7}$,
c28=773,c29=801,
∴公共项28项,
∴公共项的总和:${S}_{28}=28×17+\frac{28×27}{2}×28$=11060.
点评 本题考查等差数列的前n项和的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | a>b>c | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
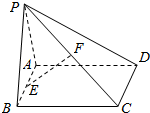 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
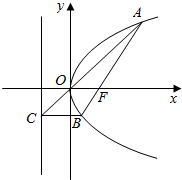 过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.
过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com