
设平面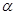 的一个法向量为
的一个法向量为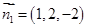 ,平面
,平面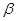 的一个法向量为
的一个法向量为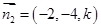 ,
,
若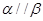 ,则k= ( )
,则k= ( )
A.2 B.-4 C.-2 D.4
 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| 3 |
| n |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2010年上海市普陀区高考数学二模试卷 (理科)(解析版) 题型:解答题
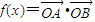 .
.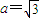 ,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;
,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;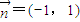 的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;
的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;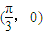 对称,且在
对称,且在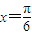 处f(x)取得最小值”.
处f(x)取得最小值”.查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二4月月考理科数学试卷(解析版) 题型:解答题
如图,在正方体 中,
中,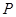 是棱
是棱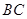 的中点,
的中点,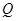 在棱
在棱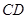 上.
上.
且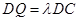 ,若二面角
,若二面角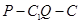 的余弦值为
的余弦值为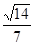 ,求实数
,求实数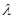 的值.
的值.
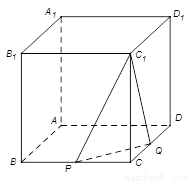
【解析】以A点为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,设正方体的棱长为4,分别求出平面C1PQ法向量和面C1PQ的一个法向量,然后求出两法向量的夹角,建立等量关系,即可求出参数λ的值.
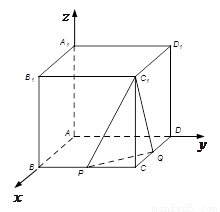
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com