Question

【题目】如图，已知在四棱锥中，底面是边长为4的正方形，是正三角形，平面平面，分别是的中点.

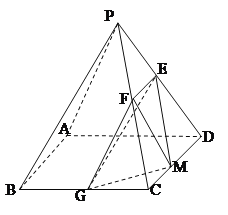
（1）求证：平面平面；

（2）若是线段上一点，求三棱锥的体积.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题分析：（1）要证明面面垂直，只需在一个平面内找到另一平面的一条垂线.由已知平面平面，且，可证平面，再根据是中位线，可证，从而平面，进而再证平面平面，该题实质是先找到面的一条垂线，再将平移到面内；

（2）点是线段的动点，考虑到和到面的距离相等，故，再结合第（1）问结果，取的中点连接，据面面垂直的性质，点到的距离就是三棱锥的高，再求，进而求体积.

试题解析：（1）∵平面平面，平面平面，平面，，平面，又中，分别是的中点，，可得平面，平面，∴平面平面；

（2），平面，平面，平面，因此上的点到平面的距离等于点到平面的距离，∴，取的中点连接，则，平面，平面，∴，于是，

∵平面平面，平面平面，是正三角形，∴点到平面的距离等于正的高，即为，因此，三棱锥M﹣EFG的体积==.