
����Ŀ��������M���㣺x��y��M������x+y��M��xy��M����Ƽ���M�Ƿ�յģ���Ȼ��������Z����������Q���Ƿ�յģ����ڷ�յļ���M��MR����f��M��M�ǴӼ��ϵ����ϵ�һ�������� ���������f��x+y��=f��x��+f��y�����ͳ��DZ��ӷ��ģ�
�����x��y��M����f��xy��=f��x��f��y�����ͳ�f�DZ��˷��ģ�
�����f���DZ��ӷ��ģ����DZ��˷��ģ��ͳ�f��M���DZ�����ģ�
�����������£����� ![]() ��յģ���ǡ�����������f��x����Q�ϱ����㣬�����Dz���Ϊ��ĺ�������д������������һ������f��x��= ��
��յģ���ǡ�����������f��x����Q�ϱ����㣬�����Dz���Ϊ��ĺ�������д������������һ������f��x��= ��
���𰸡��ǣ�f��x��=x��x��Q
���������⣺��x= ![]() m+n��y=
m+n��y= ![]() a+b��m��n��a��b��Q�� ��x+y=
a+b��m��n��a��b��Q�� ��x+y= ![]() m+n+
m+n+ ![]() a+b=
a+b= ![]() ��m+a��+��n+b����m+a��n+b��Q��
��m+a��+��n+b����m+a��n+b��Q��
��f��x+y��=f��x��+f��y����
��xy=�� ![]() m+n����
m+n���� ![]() a+b��=3ma+
a+b��=3ma+ ![]() ��mb+an��+bn=
��mb+an��+bn= ![]() ��mb+an��+��bn+3ma����mb��an��bn��3ma��Q��
��mb+an��+��bn+3ma����mb��an��bn��3ma��Q��
��f��xy��=f��x��f��y����
�����������£����� ![]() �Ƿ�յģ�
�Ƿ�յģ�
��f��x��=x��x��Q����������
��m��n��Q��
��f��m+n��=m+n=f��m��+f��n����
f��mn��=mn=f��m��f��n����
���Դ��ǣ��ǣ�f��x��=x��x��Q


 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=ax2+bx��1����0��f��1����1����2��f����1����0����z= ![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2��lnx��a��R��
��1����a=1ʱ������f��x���ڵ� ��1��f��1�����������߷��̣�
��2���Ƿ����ʵ��a��ʹf��x������СֵΪ ![]() �������ڣ����a��ֵ���������ڣ���˵�����ɣ�
�������ڣ����a��ֵ���������ڣ���˵�����ɣ�
��3����x�ʣ�0��+�ޣ�ʱ����֤��e2x3��2x��2��x+1��lnx��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��g��x��=x2eax��a��0���� ��������f��x���ĵ������䣻
��g��x��=x2eax��a��0���� ��������f��x���ĵ������䣻
������������x1 �� x2��[0��2]��f��x1����g��x2�����������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=ln��x��1��+ax2+x+1��g��x��=��x��1��ex+ax2 �� a��R�� ����a=1ʱ������f��x���ڵ㣨2��f��2�����������߷��̣�
����������g��x����������㣬����a��ȡֵ��Χ��
����֤��f��x����g��x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���A��B��C�ĶԱ߷ֱ���a��b��c�����㣨2a��c��cosB=bcosC��
��1�����B�Ĵ�С��
��2������ABC�����Ϊ ![]() ����a+c��ֵ��
����a+c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABC�У�����ABC�DZ߳�Ϊ6���������Σ�PA�͵���ABC����PB�����ABC���ɵĽ�Ϊ ![]() ��
�� 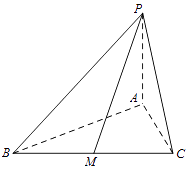
��1��������P��ABC�������
��2����M��BC���е㣬������ֱ��PM��AB���ɽǵĴ�С������÷����Ǻ���ֵ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ����С������Ϊ�У�
����С������Ϊ�У�
������f��x���ĵ����������䣻
������a��b��c�ֱ�Ϊ��ABC�����ڽ�A��B��C�ĶԱߣ���A����ǣ�f��A��=0��a=1��b+c=2�����ABC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com