
分析 由等比数列前n项和公式推导出Tn=9-2n-$\frac{8}{{2}^{n}}$,由此能示出数列{Tn}最大项的值.
解答 解:∵数列{an}是等比数列,公比q=2,Sn为{an}的前n项和,
Tn=$\frac{9{S}_{n}-{S}_{2n}}{{a}_{n+1}}$(n∈N*),
∴Tn=$\frac{9•\frac{{a}_{1}(1-{2}^{n})}{1-2}-\frac{{a}_{1}(1-{{2}^{2n})}_{\;}}{1-2}}{{a}_{1}•{2}^{n}}$=9-2n-$\frac{8}{{2}^{n}}$,
∵${2}^{n}+\frac{8}{{2}^{n}}≥2\sqrt{{2}^{n}•\frac{8}{{2}^{n}}}$=4$\sqrt{2}$,
当且仅当${2}^{n}=\frac{8}{{2}^{n}}$时取等号,
又n∈N*,n=1或2时,Tn取最大值T1=9-2-4=3.
∴数列{Tn}最大项的值为3.
故答案为:3.
点评 本题考查数列中最大项的值的求法,是中档题,解题时要认真审题,注意等比数列性质、基本不等式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
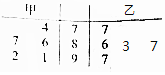 某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.
某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若m⊥α,m⊥β,则α∥β | C. | 若m⊥β,α⊥β,则m∥α | D. | 若n⊥m,n⊥α,则m∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{24}$,0) | B. | ($\frac{5π}{24}$,0) | C. | ($\frac{11π}{24}$,0) | D. | ($\frac{11π}{12}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110° | B. | 70° | C. | 20° | D. | 160° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com