练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (1)已知f(cosx)=cos17x,,求证:f(sinx)=sin17x;

    (2)对于怎样的整数n,才能由f(sinx)=sinnx推出f(cosx)=cosnx?

    (1)证明:f(sinx)=f［cos(-x)］=cos［17(-x)］=cos(8π+-17x)=cos(-17x)=sin17x,

    即f(sinx)=sin17x.

    (2)解:f(cosx)=f［sin(-x)］=sin［n(-x)］=sin(-nx)

    =

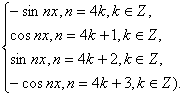
    故所求的整数n=4k+1(k∈Z).

    点评:正确合理地运用公式是解决问题的关键所在.对诱导公式的应用需要较多的思维空间，要善于观察题目特点，灵活变形.观察本例条件与结论在结构上类似,差别在于一个含余弦,一个含正弦,注意到正弦、余弦转化可借助sinx=cos(-x)或cosx=sin(-x).要善于观察条件和结论的结构特征,找出它们的共性与差异;要注意诱导公式可实现角的形式之间及互余函数名称之间的转移.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f（x）=
    m
    •
    n
    ，其中
    m
    =(sinωx+cosωx，
    		3
    cosωx)    ，
    n
    =（cosωx-sinωx，2sinωx）（ω＞0）．若f（x）图象中相邻的对称轴间的距离不小于
    π
    2
    ．
    （1）求ω的取值范围
    （2）在△ABC中，a，b，c分别为角A，B，C的对边．且a=
    		3
    ，b+c=3，f（A）=1，当ω最大时．求△ABC面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知
    m
    =(cosωx，sinωx)(ω＞0)，
    n
    =(1，
    		3
    )    ，若函数f(x)=
    m
    •
    n
    的最小正周期是2，则f（1）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=tan(
    π2
    -x)tan(π+x)+sin(-x)cos(π+x)    ．
    （1）化简f（x）；
    （2）当tanx=2时，求f（x）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=
    cosπx(x＜1)
    f(x-1)-1(x＞1)
    则f(
    1
    3
    )+f(
    4
    3
    )    =
    0
    0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （实验班必做题）
    （1）
    1
    2sin170°
    -2sin70°    =
     
    ；
    （2）若
    π
    4
    ＜x＜
    π
    2，
    则函数y=tan2xtan3x的最大值为
     
    ；
    （3）已知f（x）=2sin（x+
    θ
    2
    ）cos（x+
    θ
    2
    ）+2
    		3
    cos2（x+
    θ
    2
    ）-
    		3
    ，若0≤θ≤π，使函数f（x）为偶函数的θ为
     

    A、
    π
    6
       B、
    π
    4
       C、
    π
    3
        D、
    π
    2
    ．

    查看答案和解析>>

    同步练习册答案