
���� �����������Ķ��壬����P��x0��y0����Ax1+By1+C�ķ��ţ��ֱ��ֱ��P1P2��ֱ��l��λ�ù�ϵ�����жϣ�
��� �⣺���ڢ٣���d1-d2=0������d1=d2����Ax1+By1+C=Ax2+By2+C��
����d1=d2=0ʱ����Ax1+By1+C=Ax2+By2+C=0��
���P1��P2����ֱ��l�����ʱֱ��P1P2��ֱ��l�غϣ���ٴ���
���ڢڣ��ɢ�֪����d1=d2=0ʱ������d1+d2=0��
����ʱAx1+By1+C=Ax2+By2+C=0��
���P1��P2����ֱ��l�����ʱֱ��P1P2��ֱ��l�غϣ���ڴ���
���ڢۣ���d1•d2��0������Ax1+By1+C����Ax2+By2+C����0��
���P1��P2�ֱ�λ��ֱ��l��ͬ�࣬��ֱ��P1P2��ֱ��l�ཻ��ƽ�У������ȷ��
���ڢܣ���d1•d2��0������Ax1+By1+C����Ax2+By2+C����0��
���P1��P2�ֱ�λ��ֱ��l�����࣬��ֱ��P1P2��ֱ��l�ཻ�������ȷ��
�ʴ�Ϊ���ۢܣ�
���� ������Ҫ������ֱ�߾����йص�������жϣ����������Ƴ�����ֱ�ߵ�λ�ù�ϵ�ǽ������Ĺؼ����ۺ��Խ�ǿ���������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��0��n��0 | B�� | m��0��n��0 | C�� | m��0��n��0 | D�� | m��0��n��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a^3}{6}$ | B�� | $\frac{a^3}{12}$ | C�� | $\frac{{\sqrt{3}{a^3}}}{12}$ | D�� | $\frac{{\sqrt{2}{a^3}}}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{100}+\frac{y^2}{96}=1$ | B�� | $\frac{x^2}{25}+\frac{y^2}{21}=1$ | C�� | $\frac{x^2}{96}+\frac{y^2}{100}=1$ | D�� | $\frac{x^2}{21}+\frac{y^2}{25}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��b��a�Φ�����b�Φ� | B�� | ��a��b��a�ͦ�����b�ͦ� | ||
| C�� | ��a�Φ���a�Φ£����ɦ�=b����a��b | D�� | ��a�Φ������ͦ£���a�ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
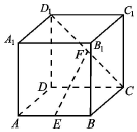 ������ABCD-A1B1C1D1�У�EΪAB�е㣬FΪCD1�е㣮
������ABCD-A1B1C1D1�У�EΪAB�е㣬FΪCD1�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{{��^2}+4}$ | B�� | �� | C�� | 2 | D�� | $\sqrt{{��^2}+1}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com